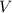 призмы =
призмы = 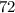 см³.
см³.
Обозначим данную призму буквами 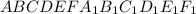 .
.
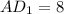 см.
см.
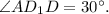
============================================================
Если призма правильная, то она всегда будет прямой.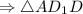 - прямоугольный, где
- прямоугольный, где 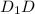 - высота данной призмы.
- высота данной призмы.
Рассмотрим 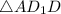 :
:
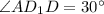 , по условию.
, по условию.
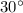 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.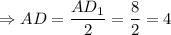 см.
см.
По теореме Пифагора найдём высоту 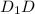 :
:
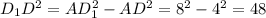
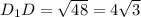 см.
см.
Рассмотрим нижнее основание данной призмы:
шестиугольник 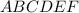 - правильный, так как данная призма тоже правильная.
- правильный, так как данная призма тоже правильная.
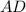 - большая диагональ шестиугольника
- большая диагональ шестиугольника 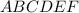 .
.
По свойству правильного шестиугольника, 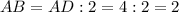 см.
см.
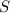 шестиугольника =
шестиугольника = 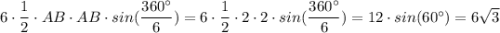 cм².
cм².
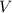 призмы =
призмы = 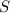 шестиугольника
шестиугольника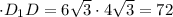 см³
см³
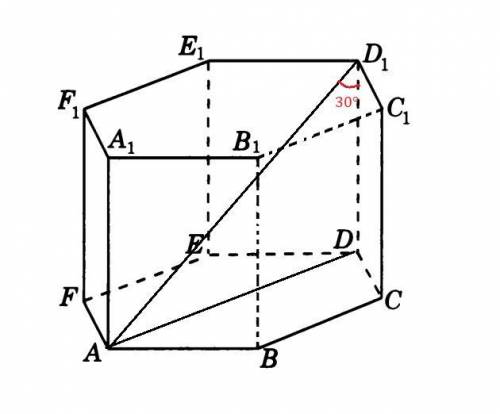
Из точки С проводим отрезок СЕ, равный и параллельный диагонали ВД.
Получаем треугольник АСЕ, равный по площади трапеции.
АК = √(13² - 5²) = √(169 - 25) = √144 = 12.
КЕ = √(41-25) = √16 = 4.
Сторона АЕ = 12 + 4 = 16.
Тогда площадь треугольника и трапеции равна:
S = (1/2)*16*5 = 40 кв.ед.