В равнобедренном треугольнике углы при основании равны, в треугольнике не может быть двух тупых углов, следовательно только угол против основания может равен 120.
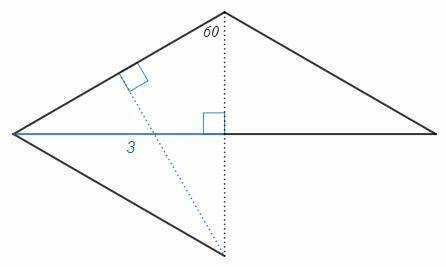
Серединный перпендикуляр к основанию равнобедренного треугольника является также биссектрисой - делит угол против основания на два угла по 60, и медианой - делит основание на два отрезка по 3.
Точка пересечения серединных перпендикуляров является вершиной равнобедренного треугольника с основанием на боковой стороне (любая точка серединного перпендикуляра равноудалена от концов отрезка). Равнобедренный треугольник с углом 60 - равносторонний. В равностороннем треугольнике высоты равны.
Расстояние от точки пересечения серединных перпендикуляров до боковой стороны равно 3.
Расстояния от точки М до вершин квадрата одинаковы и равны 3 см
Объяснение:
Смотри рисунок на прикреплённом фото.
Сторона квадрата а = 4см.
Диагональ квадрата d = a√2 = 4√2 (см)
Половинки диагоналей квадрата ОА = ОВ = ОС = ОК = d/2 = 2√2 cм
Рассмотрим прямоугольный ΔМОС
По теореме Пифагора МС² = ОМ² + ОС² = 1² + (2√2)² = 9
Тогда МС = √9 = 3 (см)
Поскольку проекции на плоскость АВСК наклонных МА, МВ, МС и МК, которыми являются половинки диагоналей, равны между собой, (ОА = ОВ = ОС = ОК), то и наклонные тоже равны МА = МВ = МС = МК = 3см.