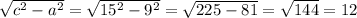
68. По данным на рисунке найдите площадь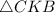 
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :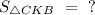
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,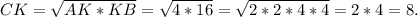 
Следовательно,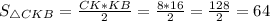 
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите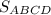 
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,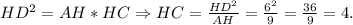 
Следовательно,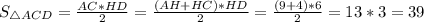 
ед².
Тогда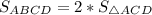 
= 2*39 ед² = 78 ед².
78 ед².
Объяснение:
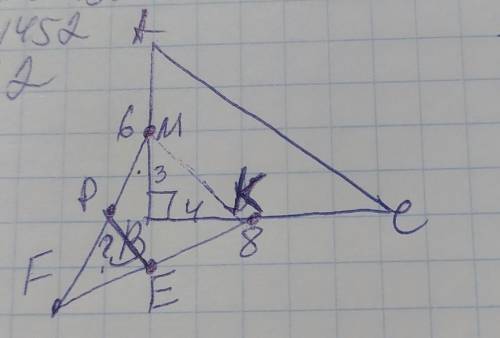
Пусть точка М лежит на стороне АВ, точка К на стороне ВС, точка Р на FM, а точка Е на FK Соединим точки М и К получился отрезок МК и прямоугльный ∆ВМК, у которого с ∆АВС общий прямой угол В и ВМ и ВК - катеты, а МК - гипотенуза. Так как точки М и К взяты с середин сторон, то ВМ=6÷2=3см, а ВК=8÷2=4см. Найдём гипотенузу МК по теореме Пифагора:
МК²=ВМ²+ВК²=3²+4²=9+16=25; МК=√25=5см.
Рассмотрим полученный ∆МFE. Так как Р и Е - середины отрезков FM и FK, то РЕ параллельна МК и является её средней линией, и по свойствам средней линией треугольника РЕ=½МК=5/2=2,5см
ответ: РЕ=2,5см
9²+d²=15²
81+d²=225
d²=225-81
d²=144
d=√144
d=12 см (катет)