1. Найдите площадь равнобедренного треугольника по боковой стороне и высоте, опущенной на основание, которые равны соответственно 5 см и 2 см.
1/2 основания = √(5^2-2^2)=√21
основание = 2√21
площадь= 1/2 основание*высота = 1/2*2√21*2=2√21 см2
ответ 2√21 см2
2
3
4
Из правил сервиса: "Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач".
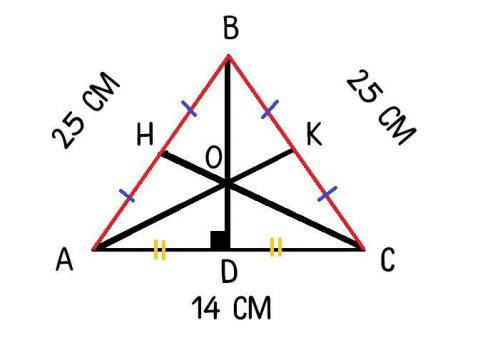
Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC = 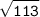 см
см
по свойству медианы 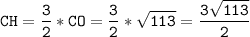 см
см
по свойству равнобедренного треугольника CH=AK= 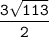 см
см
ответ: 24 см; 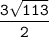 см;
см; 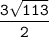 см
см
а) диагонали ромба взаимно перпендикулярны
б) точкой пересечения делятся пополам. (8 и 15)
в) при пересечении образуют 4 равных прямоугольных треугольника.
Собирая все это, понимаем, что надо найти гипотенузу этих треугольников. Это и будет сторона ромба. (По теореме Пифагора она равна 17).
ответ: 17