Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
ответ: 25 + 10√7 ≈ 51,46 см2 .
Придется воспользоваться теоремой косинусов.
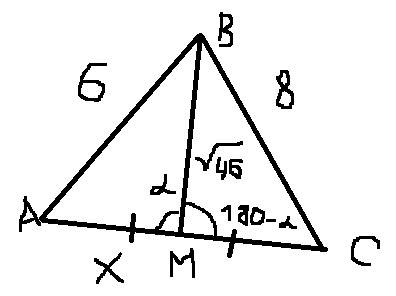
Смотри рисунок. Обозначим BM - медиана, AM=x см,
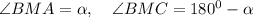
Выразим АВ по теореме косинусов через треугольник АВМ.
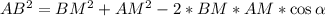
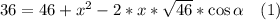
Выразим ВC по теореме косинусов через треугольник ВCМ.
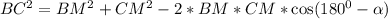
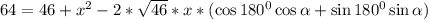
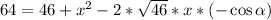
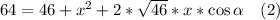
Составим систему уравнений из (1) и (2)
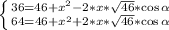
Нам нужно найти x. Поэтому надо избавиться от второго неизвестного. Поступим следующим образом. Вычтем из второго уравнения первое и выразим слагаемое с переменной альфа.
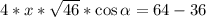
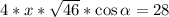
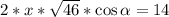
Теперь подставим верхнее значение слагаемого с альфа в первое уравнение системы
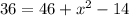
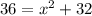
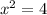
x=2.
Значит
АС=2*х
АС=2*2
АС=4
ответ: 4
а)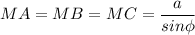
б)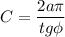
в)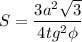
Объяснения:
Пусть К, Н и Р - середины сторон АВ, ВС и АС соответственно, тогда
АН⊥ВС, ВР⊥АС, СК⊥АВ (треугольник правильный, медианы, высоты и биссектрисы совпадают).
Центр О правильного треугольника АВС равноудален от вершин и от сторон треугольника, т.е.
АО = ВО = СО, КО = НО = РО, а эти отрезки - проекции соответствующих наклонных на плоскость треугольника, значит
МА = МВ = МС - расстояния от точки М до вершин
и МК = МН = МР - расстояния от точки М до сторон (МК⊥АВ, МН⊥ВС, МР⊥АС по теореме о трех перпендикулярах).
а) ΔМОС: ∠МОС = 90°,
___
____
Из прямоугольного треугольника МОК по теореме Пифагора:
___
____
б) СО - радиус описанной окружности. Тогда длина окружности:
_____
в)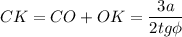
Площадь правильного треугольника АВС: