Відстань від точки А до центра кола дорівнює 11,2 см
Объяснение:
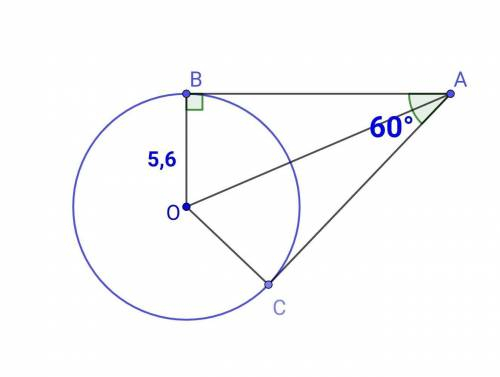
З точки А до кола з центром О проведено дві дотичні АВ і АС (В і С- точки дотику). Радіус кола дорівнює 5,6 см, ∠ВАС = 60°. Чому дорівнює відстань від точки А до центра кола?
Дотична до кола перпендикулярна радіусу, проведеному в точку дотику. Катет прямокутного трикутника, що лежить навпроти кута кута 30°, дорівнює половині гіпотенузи. Розв'язання1) ОВ=ОС=R, АВ⟂ОВ, АС⟂ОС - як дотичні до кола, тому △АВО і △АСО - прямокутні.
2) △АВО=△АСО за гіпотенузою і катетом (ОВ = ОС як радіуси, АО - спільна)
⇒ ∠ВАО=∠САО=∠ВАС : 2 = 60° : 2 = 30°.
3) В прямокутному трикутнику АВО катет ВО лежить навпроти кута ∠ВАО=30°, отже:
ВО = ½ • АО
АО = 2 • ВО = 2 • 5,6 = 11,2 (см)
Відповідь: 11,2 см
#SPJ1
2) Треугл. АОС подобен треугольнику ЕОМ по 3 углам (угол ЕОМ = углу АОС, как вертикальные углы; угол ЕМО = углу ОАС, как накрест лежащие углы при парал. прямых ЕМ и АС и секущей АМ; угол ЕМО = углу ОСА, как накрест лежащие углы при парал. прямых ЕМ и АС и секущей СЕ)
Следовательно, АС/ЕМ=ОС/ОЕ; 24/12=OC/3; ОС=24*3/12=6