1) нет
2) да
3) нет
4) нет
5) нет
6) нет
7) нет
8) нет
9) нет; да
10) да
11) нет; да
13) да
14) нет
15) 16) да; да
Объяснение:
Параллелограмм - четырехугольник, у которого стороны попарно паралелльны
Свойства параллелограмма:
1) Противолежащие стороны и углы равны
2) Диагонали точкой пересечения делятся попол
ам
3) Биссектриса угла параллелограмма образует р/б ∆
Прямоугольник - параллелограмм, у которого все углы прямые
Свойства прямоугольника:
Те же, что и у параллелограмма 1) 2)
4) Диагонали прямоугольника равны
Ромб - параллелограмм, у которого все стороны равны
Свойства ромба:
Те же, что и у параллелограмма 1) 2)
5) Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Квадрат - прямоугольник, у которого все стороны равны
Свойства квадрата:
Те же, что и прямоугольника и ромба 1) 2) 4) 5)
|AC| = 10 см.
Объяснение:
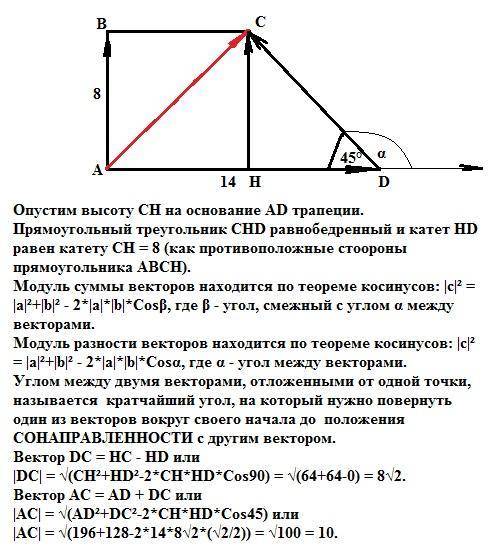
Опустим высоту СН на основание AD трапеции.
Прямоугольный треугольник СНD равнобедренный и катет HD равен катету СН = 8 (как противоположные стоороны прямоугольника АВСН).
Модуль суммы векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosβ, где β - угол, смежный с углом α между векторами.
Модуль разности векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosα, где α - угол между векторами.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения СОНАПРАВЛЕННОСТИ с другим вектором. Итак,
Вектор DC = НС - HD или
|DC| = √(CH²+HD²-2*CH*HD*Cos90) = √(64+64-0) = 8√2.
Вектор АС = AD + DC или
|AC| = √(AD²+DC²-2*CH*HD*Cos45) или
|AC| = √(196+128-2*14*8√2*(√2/2)) = √100 = 10.
ответ: Длина вектора (модуль) АС = 10 см.
Отношение площадей равно ( π16²)/(π16) = 16.
Значит, радиус сечения равен Ro/(√16) = 16/(√= 16/4 = 4.
В осевом сечении радиусы - это катеты в подобных треугольниках с коэффициентом подобия 4:16 = 1:4.
Тогда высота конуса равна 5*4 = 20.