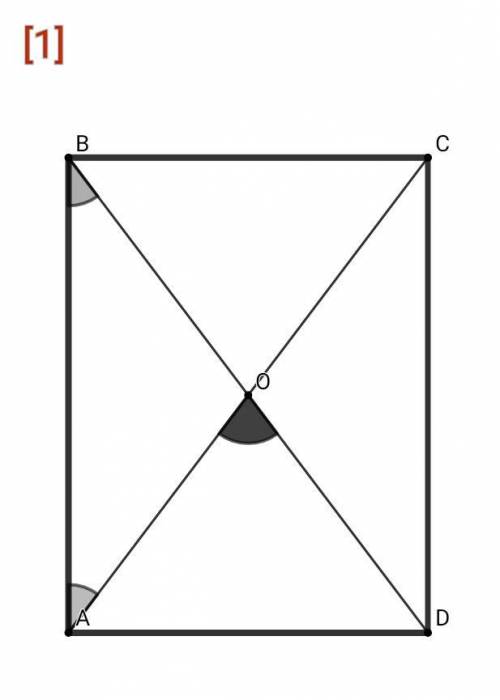
По свойству прямоугольника его диагонали равны и точкой пересечения делятся пополам, при этом образуя две пары равных и равнобедренных треугольников ⇒ АО = СО = ВО = ОD ⇒ ΔAOB - равнобедренный, так как АО = ВО. Углы при основании равнобедренного треугольника равны: ∠АВО = ∠ВАО = 36°
∠АОD = ∠ABO + ∠BAO = 2•∠ABO = 2•36° = 72° - по свойству внешнего угла ∠АОD
ответ: 72°
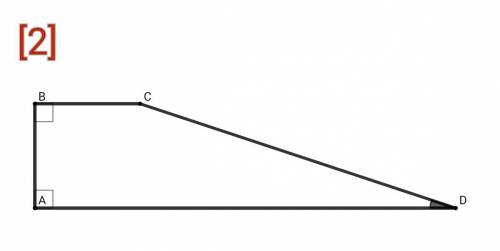
[2]Найдите углы прямоугольной трапеции, если один из углов равен 20°.В прямоугольной трапеции присутствуют два прямых угла при одной боковой стороне, при другой - острый и тупой угол ⇒ ∠ADC = 20°, ∠ABC = 90° , ∠BAD = 90°. Сумма углов в четырёхугольнике составляет 360° ⇒ ∠BCD = 360° - 90° - 90° - 20° = 180° - 20° = 160°
ответ: 20° , 90° , 90° , 160°
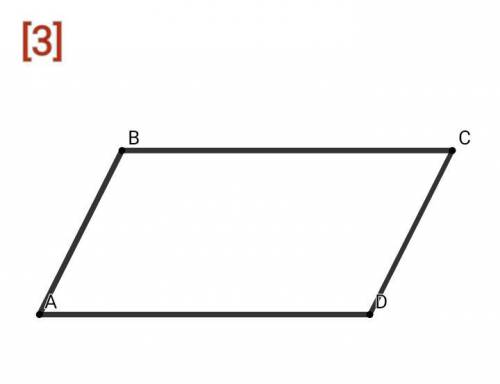
[3]Стороны параллелограмма относятся как 1:2, а его периметр равен 30 см. Найдите стороны параллелограмма.По свойству параллелограмма его противолежащие стороны попарно параллельны и равны ⇒ AB = CD , BC = AD
Пусть AB = x, тогда BC = 2x, составим уравнение:
P (abcd) = 2•(AB + BC)
30 = 2•(x + 2x) ⇒ 6x = 30 ⇒ x = 5 см
Значит, AB = CD = 5 см, BC = AD = 2•5 = 10 см
ответ: 5 см, 10 см, 5 см, 10 см
[4]В равнобедренной трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.По свойству равнобедренной трапеции углы при его основаниях равны ⇒ ∠АВС = ∠BCD , ∠BAD = ∠CDA
По условию ∠BAD + ∠CDA = 96° ⇒ 2•∠BAD = 96° ⇒ ∠BAD = ∠CDA = 48°
Сумма углов в четырёхугольнике составляет 360° ⇒ ∠ABC + ∠BCD = 360° - 48° - 48° ⇒ ∠ABC + ∠BCD = 264° ⇒ 2•∠ABC = 264° ⇒ ∠ABC = ∠BCD = 132°
ответ: 48° , 48° , 132° , 132°
[5]Высота ВМ, проведенная из вершины угла ромба АВСD образует со стороной АВ угол в 30°, АМ = 4 см. Найдите длину диагонали ВD ромба, если точка М лежит на стороне АD.В прямоугольном ΔАВМ: катет, лежащий против угла в 30°, равен половине гипотенузы ⇒ АВ = 2•АМ = 2•4 = 8 см
Сумма углов в треугольнике составляет 180°: ∠ВАМ = 180° - 90° - 30° = 60°
В ромбе все стороны равны: АВ = ВС = CD = AD = 8 см
ΔBAD - равнобедренный, так как AB = AD = 8 см. В равнобедренном треугольнике углы при основании равны: ∠ABD = ∠ADB = (180° - ∠BAD)/2 = (180° - 60°)/2 = 60° ⇒ ∠BAD = ∠ABD = ∠ADB = 60°
Значит, ΔABD - равносторонний, AB = AD = BD = 8 см
ответ: 8 см


Объяснение:<!--c-->
image
1. Так как дан правильный тетраедр, то независимо от данных граней искомое сечение будет являться равносторонним треугольником MNK. При построении этого сечения необходимо провести параллельные отрезки каждой стороне грани ADB, которая по определению правильного тетраэдра — равносторонний треугольник. Таким образом искомое сечение тоже является равносторонним треугольником, подобным треугольнику ADB.
2. Рассмотрим рисунок грани DCB, через центр O которой мы проводим сторону сечения NK.
image
3. Центр равностороннего треугольника находится в точке пересечения высот, биссектрис и медиан и делит медиану (которая также является высотой и биссектрисой) в отношении 2:1, другими словами отношение большой части медианы к всей медиане 2:3.
4. Значит, отношение стороны сечения к ребру тетраэдра также 2:3.
5. Если обозначить ребро тетраэдра через a и сторону сечения через b, то ba=23 и b=2a3.
6. Площадь равностороннего треугольника определяется по формулеSMNK=b2⋅3√4=4⋅a2⋅3√9⋅4=a2⋅3√9=32⋅3√9
7. В результате рассчётов, площадь сечения — SMNK=1⋅3√ см2.