Сторона меньшего основания правильной треугольной усечённой пирамиды равна 2 см, а боковое ребро пирамиды, равное √2 см , образует со стороной большего основания угол 45° . Найдите полную поверхность пирамиды.
Объяснение:
S( полное)=S(в.осн.)+S(н.основ)+S(бок) ,
1) S(прав.треуг.)=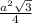 , S(в.осн.)=
, S(в.осн.)=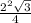 =√3 (см²).
=√3 (см²).
2)Боковые грани - равнобедренные трапеции . Пусть в трапеции
ВСС₁В₁ отрезки В₁Н, С₁К- высоты. Тогда ΔВВ₁Н-прямоугольный ,равнобедренный (∠ВВ₁Н=90°-45°=45°)⇒ВН=В₁Н=х. По т. Пифагора х²+х²=(√2)² ,х=1. Значит В₁Н=1 , ВС=ВН+НК+КС=1+2+1=4 (см).
3) S(н.осн.)=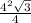 =4√3 (см²).
=4√3 (см²).
4)S(бок) =3*S(трапеции ВСС₁В₁) =3* 1/2*В₁Н*(ВС+В₁С₁)=3*1/2*1*6=9(см²).
5)S( полное)=√3 +4√3 +9=9+5√3 ( см²) .

Объем призмы равен 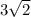
Объяснение:
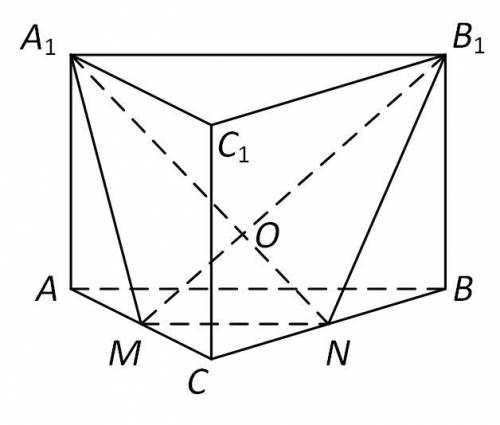
(Рис. 1)
Тт. 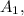
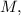
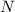 и
и 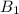 лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (
лежат в одной плоскости и, будучи соединены последовательно, образуют равнобокую трапецию (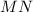 — средняя линия
— средняя линия 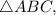 поэтому
поэтому 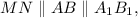
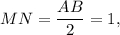
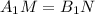 ).
).
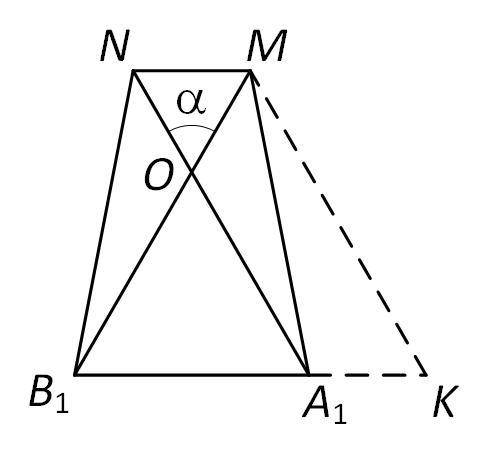
Поэтому угол, о котором идет речь в условии задачи — это угол между диагоналями трапеции.
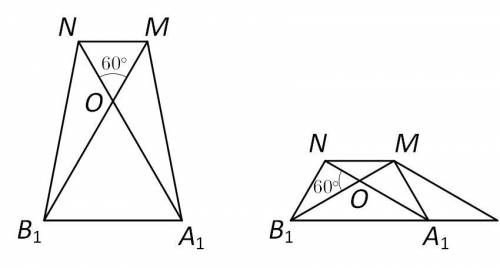
Далее возможны два варианта: 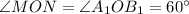 либо
либо 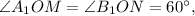 тогда
тогда 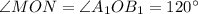 (см. рис. 2).
(см. рис. 2).
Решим задачу в общем виде (рис. 3). Пускай 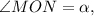
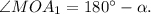 Продлим нижнее основание
Продлим нижнее основание 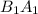 за точку
за точку 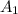 на длину верхнего основания:
на длину верхнего основания: 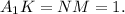 Тогда образовавшийся четырехугольник
Тогда образовавшийся четырехугольник 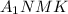 — параллелограмм,
— параллелограмм, 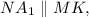
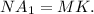 Значит
Значит 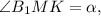 а
а
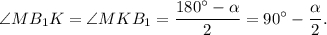
По теореме синусов
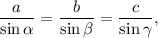
используя формулу приведения и формулу синуса двойного угла найдем длину диагонали:
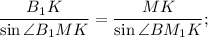
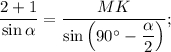
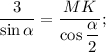
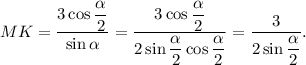
Треугольники 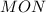 и
и 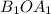 подобны,
подобны, 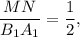 значит и
значит и 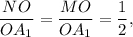 отсюда
отсюда
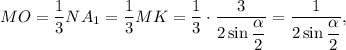
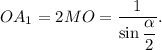
По теореме косинусов для треугольника 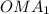
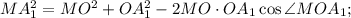
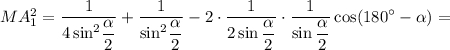
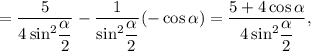
откуда
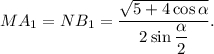
Тогда если 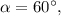
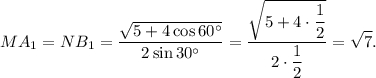
Если же 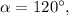 тогда
тогда
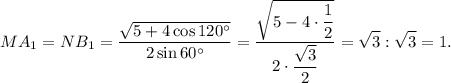
Теперь возвращаясь к призме, можем вычислить ее высоту. В прямоугольном треугольнике 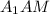 по теореме Пифагора:
по теореме Пифагора:
если 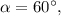
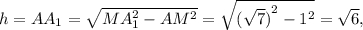
если 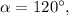
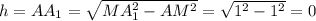
(при таком значении угла не складывается пространственная фигура — ее высота равна 0, следовательно, случай 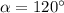 — посторонний).
— посторонний).
Площадь основания призмы вычислим по формуле площади равностороннего треугольника
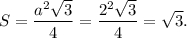
Окончательно, объем призмы:
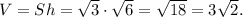
∠КLС = 180° - 145° = 35°, как смежный с данным внешним углом.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним:
∠LKC + ∠LCK = 145°,
а так как углы при основании равнобедренного треугольника равны, то
∠LKC = ∠LCK = 145° : 2 = 72,5°
ответ: 35°, 72,5°, 72,5°.