Это равнобедренная трапеция с боковыми сторонами 12, верхним 7 и нижним 9. опустим перпендикуляры из вершин меньшего основания. этими перпендикулярами нижнее основание делится на три отрезка длинами 1, 7, 1. а сама трапеция высотами делится на два одинаковых прямоугольных треугольника и прямоугольник. в прямоугольном треугольнике известны гипотенуза 12 и катет 1. по теореме Пифагора найдем второй катет (он же высота трапеции) квадратный корень из 143. найдем площадь трапеции S=(7+9)/2 × квадратный корень из 143=8корней из 143
Это равнобедренная трапеция с боковыми сторонами 12, верхним 7 и нижним 9. опустим перпендикуляры из вершин меньшего основания. этими перпендикулярами нижнее основание делится на три отрезка длинами 1, 7, 1. а сама трапеция высотами делится на два одинаковых прямоугольных треугольника и прямоугольник. в прямоугольном треугольнике известны гипотенуза 12 и катет 1. по теореме Пифагора найдем второй катет (он же высота трапеции) квадратный корень из 143. найдем площадь трапеции S=(7+9)/2 × квадратный корень из 143=8корней из 143
Дано: ∆ABC, MN || AC, MN=4см, AC=5см, BC=18см
Найти: BN - ?
Решение: 1) Докажем, что треугольники MBN и ABC подобные.
∠В - общий; так как, по условию, MN || AC, то ∠ АСВ = MNB (соответственные углы при пересечении параллельных прямых АС и MN секущей ВС).
Значит, треугольники MBN и ABC подобные.
2)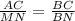 (по св-ву подобных треугольников)
(по св-ву подобных треугольников)
BN = (MN×BC)/АС=(4×18)/5=14,4.
ответ: BN = 14,4.