Окружность с центром в начале координат проходит через точку k -3 -4 найдите диаметр окружности

Question

Геометрия: Окружность с центром в начале координат проходит через точку k -3 -4 найдите диаметр окружности

petrakovatatya · Accepted Answer

а) В правильном треугольнике центры вписанной и описанной окружностей - точка пересечения медиан (биссектрис, высот, так как они совпадают).

Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. При этом больший отрезок высоты является радиусом описанной окружности, а меньший - вписанной.

r = h/3

R = 2h/3

б) Формулы, связывающие сторону правильного многоугольника с радиусами вписанной и описанной окружностей:

a(n) = 2r · tg(180°/n)

a(n) = 2R · sin(180°/n)

где a(n) - сторона правильного многоугольника, n - количество его сторон.

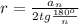
$r = \frac{a_{n}}{2tg\frac{180^{o}}{n}}$

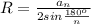
$R = \frac{a_{n}}{2sin\frac{180^{o}}{n}}$

n = 5

r = a / (2tg36°)

R = a / (2sin36°)

в) n = 6

r = a / (2tg30°) = a√3/2

R = a / (2 sin30°) = a /(2 · 1/2) = a

MOGZ ответил