3) составьте уравнения окружности с центром на оси ординат, которая проходит через точки a(-3; 0), b(0; 9)

👇

Ответ:

serg159

02.08.2020

Уравнение окружности имеет вид:
R² = (x - X₀)² + (y - Y₀)² ,
где (X₀; Y₀) - центр окружности, R - радиус
Центр окружности на оси ординат ⇒ координата X₀ = 0
Чтобы найти координату Y₀, нужно уравнять расстояния от точек А(-3;0) и В(0;9) до центра окружности O(0; Y₀)
R^2 = (x_A-X_0)^2 + (y_A-Y_0)^2=(x_B-X_0)^2+(y_B-Y_0)^2

R^2 = (x_A-X_0)^2 + (y_A-Y_0)^2=(x_B-X_0)^2+(y_B-Y_0)^2

(-3 - 0)² + (0 - Y₀)² = (0 - 0)² + (9 - Y₀)²
9 + Y₀² = 81 - 18Y₀ + Y₀²
18Y₀ = 72
Y₀ = 4
Радиус окружности равен
R^2 = (x_A-X_0)^2 + (y_A-Y_0)^2

=
= (-3 - 0)² + (0 - 4)² = 25

ответ: x² - (y - 4)² = 25

3) составьте уравнения окружности с центром на оси ординат, которая проходит через точки a(-3; 0), b

4,6(36 оценок)

Открыть все ответы

Ответ:

макс3095

02.08.2020

Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру

r=S:p

Ни площади, ни полупериметра мы пока не знаем, но можем узнать.
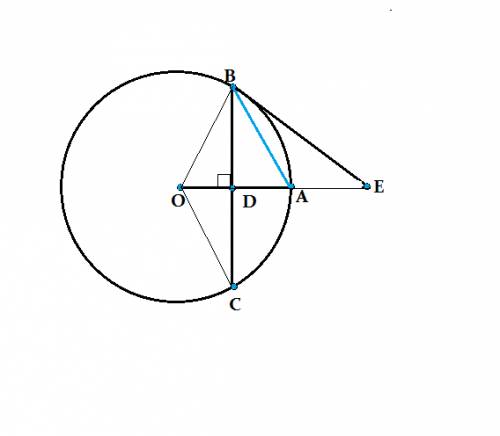
Поскольку отрезок, соединяющий центр гипотенузы с противоположным катетом перпендикулярен к нему, он от начального треугольника отрезает подобный ему.

Коэффициент подобия этих треугольников 2, так как гипотенуза вдвое больше своей половины.
Следовательно, второй катет большего треугольника равен
2,5*2=5 см
Гипотренуза равна
√ (144+25)=13 см
Площадь треугольника
12*5:2=30 см²
полупериметр

12+5+13=30 см

30:2=15 см
r=S:p=30:15=2 см

4,8(88 оценок)

Ответ:

Lizaliya

02.08.2020

Через точку D, лежащую на радиусе ОА окружности с центром О, проведена хорда ВС, перпендикулярная к ОА, а через точку В проведена касательная к опружности, пересекающая прямую ОА в точкп Е. Докажите, что луч ВА - биссектриса угла СВЕ.

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Угол АВЕ образован касательной ВЕ и хордой ВА ⇒
угол АВЕ равен половине величины дуги АВ.
Соединив О с В и С, получим равнобедренный треугольник ВОС ( образован радиусами)
Радиус ОА перпендикулярен ВС по условию и является высотой треугольника ВОС, а т.к. треугольник равнобедренный, то и биссектрисой угла ВОС; след,
∠АОС=∠АОВ, следовательно, и дуги ВА и АС, на которые опираются центральные углы АОВ и АОС, равны
Угол АВС - вписанный. Вписанный угол, опирающийся на ту же дугу, что центральный, равен половине его величины (половине величины дуги. на которую он опирается)
Угол АВС опирается на ту же дугу, что центральный ∠АОС и равен половине величины этой дуги.
Но угол АОВ опирается на дугу той же величины ( центральные углы ВОА и АОС равны, и дуги, на которые они опираются, тоже равны),
т.е.∪АВ = ∪ АС
Т.к. углы АВЕ и АВС равны половине равных дуг, ⇒ эти углы равны. Следовательно, луч ВА, делящий угол СВЕ на два равных, - биссектриса этого угла, ч.т.д.
Через точку d, лежащую на радиусе оа окружности с центром о, проведена хорда вс, перпендикулярна к о