ABCD-Ромб
Bd=13см(меньшая диагональ)
BH=12см
Найти S
у Треугольника BDH угол H=90 градусов,BD=13,BH=12cm теперь по тиареме Пифагора:
HD=Под Корнем BD(D в квадрате)-BH(Hв квадрате)=под корнем 13в квадрате-12в квадрате=5 см
теперь 2 у трегуольника ABH Угол h=90 градусов,BH=12,AH=AD-HD=(AB-5)cm теперь по теореме пифагора
AB(B в квадрате)=AH(H в квадрате)+BH(H в квадрате)
AB(B в квадрате)=(AB-5)в квадрате+12 в квадрате
AB(B в квадрате)=AB(B в квадрате)-10AB+25+144,10AB=169
AB=16.9
и Теперь Находим площадь
S=Ab умножить на BH=16,9 умножить на 12=202,8см(см в квадрате)
S=202.8см
Объяснение:
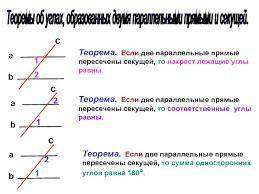
Теоремы с чертежами даны в первом рисунке
1)
a)56+32=/=180°; не параллельны
б)72=72; параллельны по накрест лежащим углам
в)113+67=180°; параллельны по сумме односторонних углов
г)153+35=/=180°; не параллельны
а)73+73=/=180°; не параллельны
б)25=/=63; не параллельны
в)58+22=/=180°; не параллельны
г)143=143; параллельны по накрест лежащим углам
2)
а) a║b
∠6=∠3=108°; ∠5=180-108=72°; ∠5=∠4=72°;
∠1=∠3=108°; ∠4=∠2=72°; ∠6=∠8=108°; ∠5=∠7=72°
б)m║d
∠4=∠6=63°; ∠3=180-63=117°; ∠3=∠5=117°; ∠7=∠5=117°; ∠6=∠8=63°; ∠2=∠3=117°; ∠1=∠4=63°
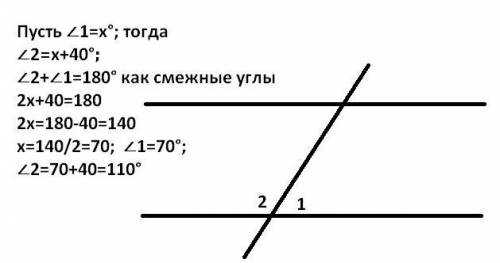
3) Решения даны на втором и третьем из прикреплённых рисунков
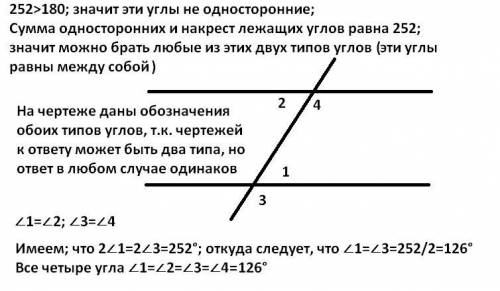
значит внутренние 180-120=60
а последний угол это 180-60-60=60
треугольник равносоторонний