ответ:Номер 1
Внешний угол и смежный ему внутренний угол в сумме составляют 180 градусов
180-109=71 градус-это внутренний угол при основании треугольника
Найдём внутренний угол при Вершине треугольника
180-153=27 градусов
Узнаём угол Х
<Х=180-(71+27)=180-98=82 градуса
ответ Б 82 градуса
Номер 2
Найдём внутренний угол при основании,внешний равен 124 градуса
180-124=56 градусов
<Х=180-(56+52)=180-108=72 градуса
ответ В 72 градуса
Номер 3
Дано:прямоугольный треугольник,биссектриса прямой угол поделила на 2 равных угла
90:2=45 градусов
Другая биссектриса из вершины треугольника поделила угол пополам,один из них искомый угол Х
Рассмотрим один из получившихся треугольников,тот где <99 градусов и угол 45 градусов
Узнаём угол при вершине этого треугольника
180-(99+45)=36 градусов
Этот угол по условию задачи равен углу Х
<Х=36 градусов
ответ:Странно,ни с одним ответом не совпадает,так это у меня один из двух одинаковых углов равен 36 градусов,а полный угол 72 градуса
Объяснение:
Дано :
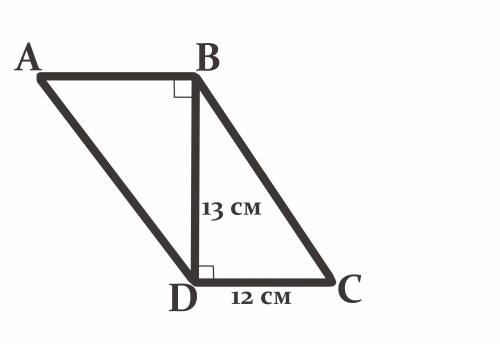
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².