76°
Объяснение:
Признак равнобедренного треугольника: если в треугольнике два угла равны, то такой треугольник - равнобедренный.
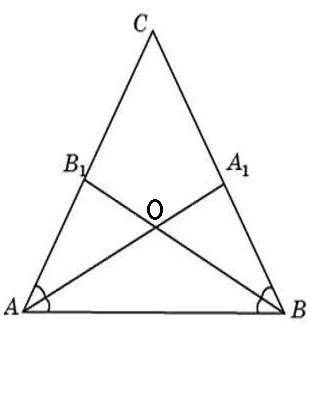
1) Рассмотрим ΔАСВ.
∠С =28°, ∠А = ∠В по условию. Т.к. сумма углов 28° Δ-ка равна 180°, то?
∠А + ∠В + ∠С = 180°, откуда
∠А + ∠В = 180° - ∠С = 180° - 28° = 152°. Но ∠А = ∠В по условию, следовательно,
∠А = ∠В = 152°/2 = 76°
2) т.к. ∠А = ∠В , а АА₁ и ВВ₁ - биссектрисы этих углов, то
∠В₁АО = ∠ОАВ = ∠А₁ВО=∠ОВА = 76°/2 = 38°
3) Рассмотрим ΔАОВ.
∠ОАВ = ∠ОВА =38°, тогда
∠АОВ = 180° -2*38° = 180° -76° = 104°
4) ∠АОВ и ∠АОВ₁ - смежные углы, их сумма = 180°, значит,
∠АОВ₁ = 180°-104° = 76°
1)на двух материках : в Северной и Южной Америке, западная часть обеих материков. между 66°градусов до 56° градусов
2) горы протянулись в направлении север-юг, длина приблизительно 12 000 км.
3) почти на всём протяжении является водоразделом между бассейнами Атлантического и Тихого океанов, а также резко выраженной климатической границей. Кордильеры лежат во всех географических поясах (кроме субантарктического и антарктического) и отличаются большим разнообразием ландшафтов и ярко выраженной высотной поясностью. Снеговая граница на Аляске - на высоте 600 м, на Огненной Земле -500-700 м в Боливии и Южном Перу поднимается до 6000-6500 м. В северо-западной части Кордильер Северной Америки и на юго-востоке Анд ледники спускаются до уровня океана, в жарком поясе они покрывают лишь наиболее высокие вершины. Общая площадь оледенений -около 90 тысяч км (в Кордильерах Северной Америки - 67 тыс. км в Андах -около 20 тыс. км)))
CD перпендикулярно AB
Рассмотрим тругольник ABC :
a^{2} + b^{2} = 5^{2} [по теореме Пифагора]
a^{2} + b^{2} = 25 [1.]
Рассмотрим треугольник ACD :
a^{2} = c^{2} + 9 [по теореме Пифагора] [2]
Рассмотрим треугольник CDB :
b^{2} = c^{2} + 4 [по теореме пифагора] [3]
Подставляем полученные уравнения в уравнение [1.] и получаем, что :
c^{2} + 9 + c^{2} + 4 = 25
2c^{2} =12
c^{2}=6
c = \sqrt{6} - отсюда находим a и b из уравнений [2] и [3]
Известны все 3 стороны треугольника, теперь можно найти косинус, синус и тангенс :
CosA = a\5 = \sqrt{0.6}
SinA = b\5 = \sqrt{0.4}
TgA = b\a = \sqrt{2 : 3}
В решении не уверен, хотя по проверкам всё сходится