ответ: AF=8, FE=9
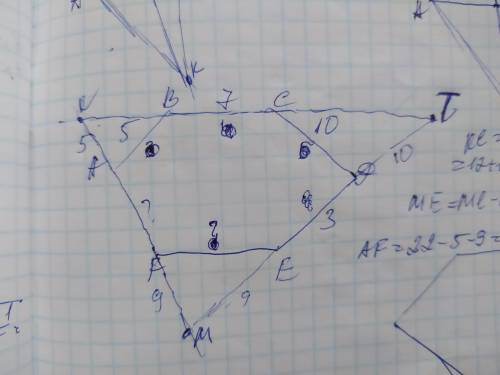
Объяснение: пусть прямая AF пересекается с прямой ВС в точке К, прямые ВС и ДЕ в точке Т, а АF и ДЕ в точке М. Получился ∆МКТ. Сумма всех углов шестиугольника составляет 180(6-2)=180×4=720° и если в нём все углы равны, то каждый из них будет 720÷6=120°. Рассмотрим полученный ∆АКВ. В нём угол А и угол В смежные с углами шестиугольника, а так как сумма смежных углов составляет 180°, то угол А=углу В=180-120°=60°. Сумма углов треугольника составляет 180°, поэтому угол К=180-60-60=60°. ∆АКВ- равносторонний, поэтому АК=ВК=АВ=5. ∆СТД и ∆FЕМ также равносторонние, так как их углы смежные с углами шестиугольника, поэтому в ∆СТД стороны СТ=ТД=СД=10, в ∆FEM стороны
FE=EM=FM. ∆МКТ - равносторонний и
КТ=ТМ=КМ=КВ+ВС+СТ=5+7+10=22.
МТ=МЕ+ЕД+ДТ
МЕ=22-3-10=9
В ∆FЕМ: FE=ME=FM=9
KM=AK+AF+FM
AF=22-9-5=8
Уравнение окружности: (х - х₀)² + (у - у₀)² = R², где О(x₀; y₀) - центр окружности; R - радиус окружности.
Так как МК - диаметр данной окружности ⇒ О (центр окружности) - середина МК.
х₀ = (М(х) + К(х))/2 = (-3 + 5)/2 = 1.
у₀ = (М(у) + К(у))/2 = (4 + 10)/2 = 7.
⇒ O(1;7)
OM = OK - радиусы данной окружности.
MK - диаметр, по условию.
МК = √((K(x) - M(x))² + (K(y) - M(y))²) = √((5 - (-3))² + (10 - 4)²) = √(64 + 36) = 10.
⇒ OM = OK = MK/2 = 10/2 = 5.
Итак, уравнение данной окружности:
(х - 1)² + (у - 7)² = 25.
Теперь, с уравнения данной окружности, найдём а:
Р(-10;а)
х = -10.
у = а.
(-10 - 1)² + (а - 7)² = 25
(-11)² + а² - 14х + 49 = 25
121 + а² - 14х + 49 = 25
170 + а² - 14х - 25 = 0
145 + а² - 14х = 0
а = -(-14) ±√(((-14)² - 4 * 1 * 145)/2 * 1
а = 14 ±√(-384)/2
а ∉ R. (а не является элементом множества R)
R - любое, положительное или отрицательное число.
ответ: а ∉ R.
Пусть AP=x, тогда PT=x
3^2=x^2+x^2
9=2x^2
4,5=x^2
X= корень из 4,5