
вчера я делал похожую задачу, посмотрите там принцип построения сечения. .см также рисунок.
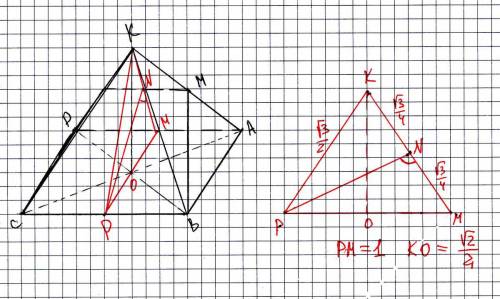
задача сводится к определению угла между боковой стороной и медианой к ней в равнобедренном треугольнике с основанием 1 и боковыми сторонами корень(3)/2.
для медианы к боковой стороне в равнобедренном треугольнике легко выводится соотношение
по теореме косинусов для МPK
b^2 = a^2 + b^2 - 2*a*b*cos(P); P - угол при основании МKP.
для медианы (2*PN)^2 = a^2 + b^2 + 2*a*b*cos(K) = 2*a^2 + b^2;
Само собой, под а и b понимаются основание и боковая сторона.
выражение для 2*PN получается из теоремы косинусов, если продолжить её за основание на свою длину и т.д... вобщем, достроить КРМ до параллелограмма и взять треугольник со сторонами 2*PN, a, b и углом (180 - P)
Отсюда PN = корень(11)/4;
Осталось вычислить cos(Ф), где Ф = угол РNM.
1 = 11/16 + 3/16 - cos(Ф)*2*корень(11*3)/16;
cos(Ф) = -1/корень(33)
Задача 1.
Объем шара находят по формуле
V=4πR³:3
Объем цилиндра находят по формуле
V= πR²h
4πR³:3=πR²h сократим одинаковые члены уравнения
h=4R:3
Задача 2.
Два равных шара расположены так, что центр одного лежит на поверхности другого.Как относится объём общей части шаров к объёму одного шара?
Объем шара
V=4 π R³:3
Объем шарового сегмента
V=π h²( R−1/3 h)
объём общей части шаров= 2 π h²( R−1/3 h
Отношение ообъема бщей части к объему одного шара
2 π h²( R−1/3 h)
4 π R³:3
После сокращения получим
h²( R−1/3 h)3
2 R³
Но высота сегмента здесь равна половине радиуса,
вместо h нужно подставить ¹/₂ R и затем упростить.
⅟₄ R² ( R−1/6 R)3
2 R³