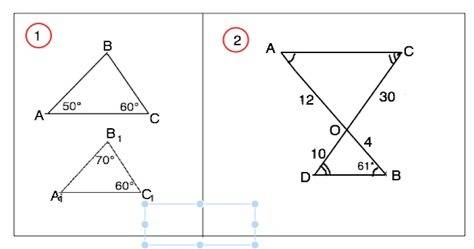
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
Задача с неполным условием, имеет бесконечно много решений в зависимости от формы треугольника. Рассмотрим три возможных варианта.
1) ΔABC - равнобедренный, AC = AB; AM=13 см; AC = 17 см
AM - медиана, в равнобедренном треугольнике одновременно высота ⇒
CM = MB; AM ⊥ CB
ΔAMC - прямоугольный, ∠AMC=90°; AM=13 см; AC = 17 см
Теорема Пифагора :
CM² = AC² - AM² = 17² - 13² = 120 = (2√30)²
CM = 2√30 см
BC = 2 CM = 2*2√30 = 4√30 см
BC = 4√30 см
=========================================
2) ΔABC - прямоугольный; ∠BAC = 90°; AM=13 см; AC = 17 см
AM - медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
BC = 2 AM = 2*13 = 26 см;
BC = 26 см
====================================
3) ΔABC - прямоугольный, ∠ABC = 90°; AM=13 см; AC = 17 см
AM - медиана ⇒ BM = MC; BC = 2BM
Теорема Пифагора
AB² = AC² - BC² = 17² - (2BM)² = 289 - 4BM²
Теорема Пифагора для ΔABM
AB² = AM² - BM² = 13² - BM² = 169 - BM²
169 - BM² = 280 - 4BM²
3BM² = 111; BM² = 37
BM = √37 см ⇒ BC = 2BM = 2√37 см
BC = 2√37 см