Объяснение:
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см

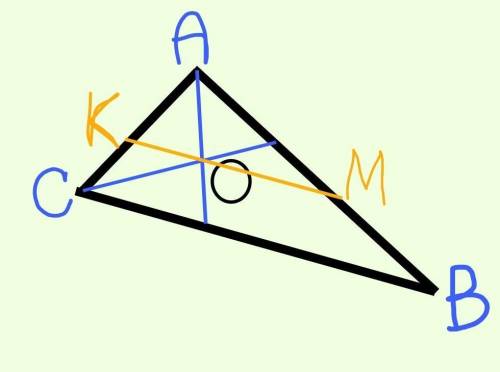
КМ – отрезок проходящий через точку пересечения биссектрис – точку О и параллельный стороне ВС по условию
По свойству отрезка проходящего через точку пересечения биссектрис и параллельный одной из сторон:
КМ=КС+МВ.
АС=1 см по условию;
АВ=2 см по условию;
АС+АВ=АК+КС+АМ+МВ
Заменим сумму КС+МВ на КМ (доказано ранее), и подставим. известные числовые значения, получим:
1+2=АК+АМ+КМ
АК+АМ+КМ=3 см
Периметр треугольника это сумма длин всех его сторон.
АК, АМ и КМ – стороны треугольника АКМ. И сумма их длин равна 3 см (найдено ранее).
Получим что периметр треугольника АКМ=3 см.
ответ: 3 см.