
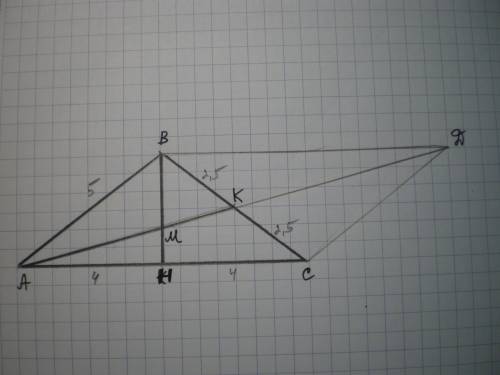
Дано: ΔАВС, равнобедренный, АВ=ВС=5 м, АС=8 м, АК - медиана, ВН - биссектриса. Найти ВМ и АК.
Найдем ВН - биссектрису, медиану и высоту по свойству равнобедренного треугольника. Рассмотрим ΔАВН - прямоугольный, АН=4 м, АВ=5 м, ВН=3 м (египетский треугольник).
Медианы треугольника в точке пересечения делятся в соотношении 2:1, считая от вершины. Поэтому ВМ=2 м.
Чтобы найти АК достроим треугольник до параллелограмма, т.к. отложим КД=АК, соединим точку Д с точками В и С.
По свойству диагоналей параллелограмма АД²+ВС²=2(АВ²+АС²); АД²+5²=2(5²+8²); АД²+25=178; АД²=153; АД=√153≈12,4 м.
АК=1\2 АД=12,4:2=6,2 м.
ответ: 2 м, 6,2 м.
Прямые, соединяющие центр вписанной окружности с концами боковой стороны - это биссектрисы внутренних односторонних углов при параллельных основаниях и секущей боковой стороне. Сумма таких углов 180 градусов, сумма половин - 90 градусов, то есть эти прямые перпендикулярны. Поэтому радиус, проведенный в точку касания этой боковой стороны, является высотой к гипотенузе в прямоугольном треугольнике. Если меньший отрезок (на который точка касания делит гипотенузу-боковую сторону) принять за х, а больший за 4*х, то высота - среднее геометрическое этих отрезков.
Действительно, высота делит прямоугольный треугольник на два подобных между собой прямоугольных треугольника - и подобных исходному, конечно - по признаку равенства углов, поэтому
4*х/12 = 12/x;
(4*х)*х = 12^2 = 144; x^2 = 36; x = 6
Боковая сторона равна 30, а периметр 120
(сумма боковых сторон равна сумме оснований)