Проведём высоты СН и DН основания пирамиды и боковой грани, соответственно. Двугранный угол при стороне основания, равный 45 градусов, это и есть линейный угол DНС.
Вершина правильной пирамиды проецируется в центр основания, в нашем случае это точка пересечения медиан (и биссектрис и высот в одном лице).
Рассмотрим ΔDОН (на рисунке - жёлтым):
Он прямоугольный, один из острых углов равен 45⁰, значит это равнобедренный треугольник, ОН=ОD=6 см.
Таким образом, высота боковой грани DH равна:
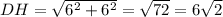 см
см
Теперь находим сторону основания.
Вспоминаем, что медианы треугольника точкой пересечения делятся на две части в отношении 2:1, считая от вершины.
Значит медиана СН=6*3=18 см
В ΔАНС (на рисунуе - зелёным) угол НСА=30⁰, значит 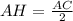
Обозначив сторону основания за Х, получим уравнение:
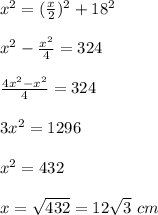
Находим площадь боковой поверхности:
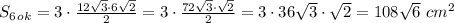
Пусть АВ = с; BC = a; AC = b;
p = (a + b + c)/2;
Я обозначаю p - c = z (в условии дано z = 3√3); или b + a - c = 2*z;
Радиус r вневписанной окружности, касающийся внешним образом стороны a, равен
r = S/(p - a); или r = 2*S/(b + c - a);
Теперь числитель и знаменятель этой дроби умножаются на 2*z = b + a - c;
r = 2*S*2*z/((b + c - a)*(b - c +a)) = 4*S*z/(b^2 - (c - a)^2) = 4*S*z/(b^2 - a^2 - c^2 + 2*a*c);
Теперь надо подставить S = a*c*sin(B)/2 и b^2 = a^2 + c^2 - 2*a*c*cos(B); получается
r = 2*z*a*c*sin(B)/(2*a*c - 2*a*c*cos(B)) = z*sin(B)/(1 - cos(B)); это ответ в общем случае.
Если подставить sin(B) = √3/2; cos(B) = -1/2, (то есть угол В = 120°) то r = z/√3;
При z = 3√3; r = 3
Это повторение моего решения вот поправкой на числа. Там еще есть немного теории про вневписанные окружности.
Я решил добавить кое-что - мало ли, кому пригодится.
Соотношение r = S/(p - a); где r - радиус вневписанной окружности, касающийся внешним образом стороны a, доказать очень просто. Если соединить центр О этой окружности с вершинами треугольника АВС, то
S = Sabo + Saco - Sbco (Sabo - это площадь треугольника АВО, и так далее)
В каждом из этих треугольников радиус вневписанной окружности является высотой к стороне, которая - к тому же - сторона треугольника АВС.
S = AB*r/2 + AC*r/2 - BC*r/2 = (c + b - a)*r/2 = (p - a)*r; где p = (a + b + c)/2;
ЧТД.
Отсюда, кстати, сразу можно получить очень веселые и красивые следствия, например, такое (с учетом формулы Герона для площади)
S^2 = r*ra*rb*rc;
где r - радиус вписанной окружности, ra, rb, rc - радиусы трех вневписанных окружностей треугольника АВС.