Под косинусом тупого угла α (90° < α < 180°) будем понимать значение косинуса смежного с ним угла, взятого со знаком минус. Косинус прямого угла будем считать равным 0.
Под синусом тупого угла будем понимать синус смежного угла. Синус прямого угла будем считать равным 1.
Из этих определений следует, что для любых углов, таких, что 0 < α < 180° справедливы равенства sin α = sin (180° – α) и cos α = –cos (180° – α).
Действительно, если α = 90°, то имеем верные равенства. sin 90° = sin (180° – 90°) и cos 90° = 0 = –cos (180° – 90°).
Если α – острый угол, то 180° – α = β, 90° < α < 180° – тупой угол. Тогда по определению sin β = sin (180° – β) или sin (180° – α) = sin (180° – (180° – α)) = sin α.
cos β = –cos (180° – β) или cos (180° – α) = –cos (180° – (180° – α)) = –cos α.
Отсюда получаем cos α = cos (180° – α).
Наконец, если α (90° < α < 180°) – тупой угол, то равенства видны по определению. думаю так.
Искомое расстояние равно 2√13 см.
Объяснение:
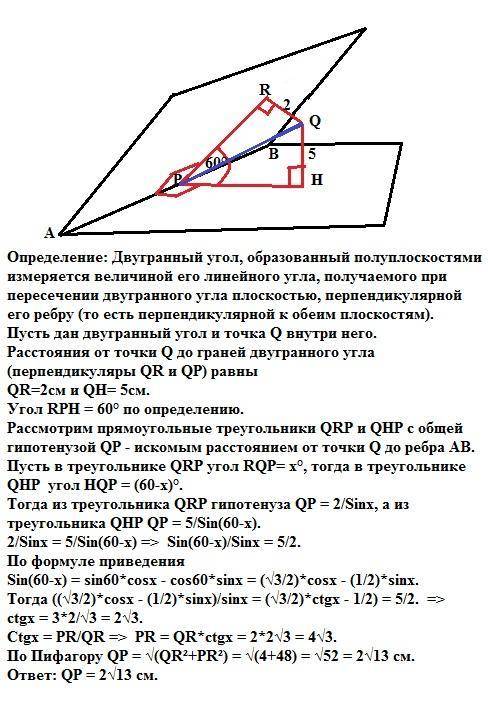
Определение: Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Пусть дан двугранный угол и точка Q внутри него.
Расстояния от точки Q до граней двугранного угла (перпендикуляры QR и QP) равны QR=2см и QH= 5см.
Угол RPH = 60° по определению.
Рассмотрим прямоугольные треугольники QRP и QHP с общей гипотенузой QP - искомым расстоянием от точки Q до ребра АВ. Пусть в треугольнике QRP угол RQP= x°, тогда в треугольнике QНP угол HQP = (60-x)°.
Тогда из треугольника QRP гипотенуза QP = 2/Sinx, а из треугольника QHP QP = 5/Sin(60-x).
2/Sinx = 5/Sin(60-x) => Sin(60-x)/Sinx = 5/2.
По формуле приведения
Sin(60-x) = sin60*cosx - cos60*sinx = (√3/2)*cosx - (1/2)*sinx.
Тогда ((√3/2)*cosx - (1/2)*sinx)/sinx = (√3/2)*ctgx - 1/2) = 5/2. =>
ctgx = 3*2/√3 = 2√3. Из треугольника QRP:
Ctgx = PR/QR (отношение прилежащего катета к противолежащему). => PR = QR*ctgx = 2*2√3 = 4√3.
По Пифагору QP = √(QR²+PR²) = √(4+48) = √52 = 2√13 см.
ответ: QP = 2√13 см.