S полн. пов=25√3 см^2
высота тетраэдра Н=(5/3)√6 см
Объяснение:
тетраэдр - правильный многогранник все грани, которого правильные треугольники, их 4.
1. S полн. пов=4×S∆
площадь правильного треугольника:
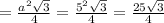
площадь полной поверхности:
S=25√3 см^2
2. рассмотрим прямоугольный треугольник
гипотенуза h - высота боковой грани тетраэдра - высота правильного треугольника
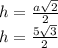
катет m -(1/3) высота основания тетраэдра - высоты правильного треугольника
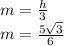
катет Н - высота тетраэдра, найти по теореме Пифагора:
Н^2=h^2-m^2
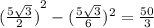
высота тетраэдра Н
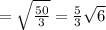

ответ: Ѕ=1 (ед. площади)
Объяснение:
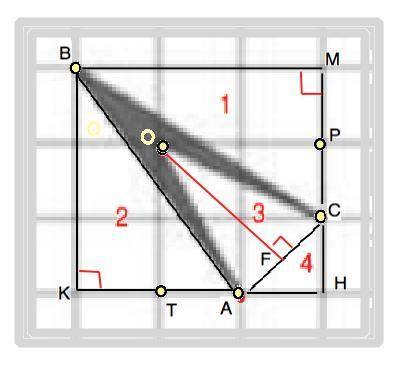
Обозначим данный невыпуклый четырехугольник АВСО и опишем около него квадрат КВМН. Найдем площадь «лишних» треугольников и вычтем из площади квадрата
Ѕ (КВМН)=3•3=9 (ед)
Площади треугольников под № 1 и №2 равны. Поэтому
Ѕ(АКВ)+Ѕ(ВМС)=2•(0,5•3•2)=6
Найдем стороны треугольника АОС (№3)
Из прямоугольного треугольника ОРС по т. Пифагора ОС=√(ОР*+РС*)=√(4+1)=√5
ОА=ОС=√5
АС=√(AH²+CH²)=√(1+1)=√2
Проведем высоту OF треугольника АОС .
По т.Пифагора OF=√(OC²-CF²)=√(18/4)=(3√2)/2
S(AOC)=OF•FC=(3√2/2)•√2/2=3/2=1,5
S(ACH=0,5•1•1=0,5
Вычитаем из площади квадрата лишнее:
Ѕ(АВСО)=9-6-1,5-0,5=1 (ед. площади).
———————
Есть формула, по которой площадь многоугольников. нарисованных на клетчатом фоне, вычисляется проще. Это формула Пика.
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Внутри многоугольника нет целочисленных точек, на границе их 4.
Ѕ=0+4/2-1=1 (ед. площади)
С = 5,1 * 3,14 = 16.014 ≈ 16см
ответ: 16см.