8,6 см
Объяснение:
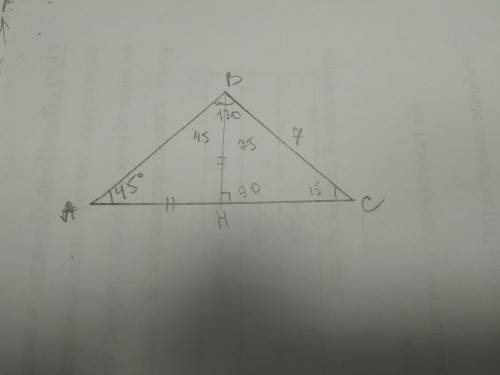
Дано: ∠А=45°, ∠В=120°, ВС=7см: Найти: АС-?
В треугольнике ∠С=180-120-45=15°
Опускаем из вершины В высоту ВН на основание АС.
В треугольнике ВНС ∠С=15°, ∠Н=90°, ∠НВС=180-15-90=75°
Высота треугольника ВН=ВС*sin∠C=7*sin15°=7*0.26=1.8(cм)
По теореме Пифагора (сумма квадратов катетов равно сумме гипотенузы) находим НС.
НС²=ВС²-ВН²=49-3,2=45,8 НС=√45,7=6,8(см)
В треугольнике АВН ∠А=45°, ∠Н=90°, ∠АВН=180-90-45=45°
Так как углы при основании равны, то получается, что треугольник АВН равнобедренный, т.е. АН=ВН=1,8 (см)
АС=АН+НС=1,8+6,8=8,6 (см)
Теорема 1. Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Теорема 2. Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Теорема 3. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Объяснение:
1) рассмотрим Δ авк ( если биссектриса- это ак):
а) углы прямоугольника равны по 90 град. ∠а=∠в=90 град.
б) тк ак- бис-са (по усл), то дедлит угол а пополам. ∠вак= 90:2=45 град.
в) сумма углов треуг. равна 180 град. ∠вка= 180-90-45=45 град.
г) в треуг. углы при основании равны. ∠а=∠к=45 град.
д) в равнобедренном треуг. боковые стороны равны. ав=вк=6см.
2) Р= 2(а+в)= 2(6+8)=2*14=28см
ответ: 28