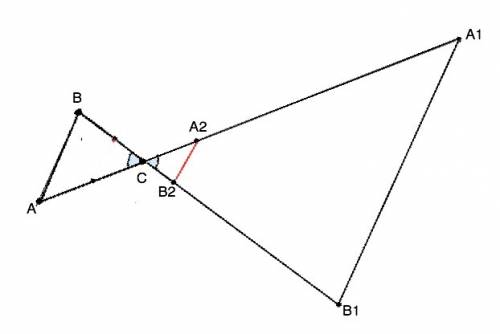
Обозначим данные точки А, В и С. Эти три точки можно соединить одним единственным в фигуру из трех точек и трех отрезков. Т.е. в треугольник , для которого предлагается построить два подобных с коэффициентом подобия k=3 и k=0,5 ( См. рисунки вложения)
Продлим ВС и АС и с циркуля 3 раза отложим длину этих сторон. Получим СА1=3АС и СВ1=3ВС. Угол А1СВ1 получившегося треугольника равен углу ВСА ( вертикальные). Треугольники АВС и А1В1С подобны по пропорциональным сторонам и равному углу между ними. Аналогично строится треугольник А2СВ2, подобный треугольника АВС с k=0,5. Для этого сначала делим две стороны пополам деления отрезка пополам циркулем Вы, конечно, уже знаете).
На сторонах угла ВАС от А циркулем на АС и АВ откладываем равные отрезки АМ и АК. Соединим М и К. На произвольной прямой отмечаем т.А1 и чертим окружность радиусом, равным АК. Точку пересечения с взятой прямой отмечаем К1. От К1 на окружности циркулем отмечаем точку М1 так, что К1М1=КМ. Из центра А1 окружности поводим прямую А1М1. Угол, равный углу ВАС исходного треугольника, построен. На прямых А1М1 и А1К1 откладываем стороны нужной длины: А1С1=3АС и А1В1=3 ВС и соединяем их. Аналогично для треугольника с k=0,5 откладываем половины длин сторон АС и АВ треугольника АВС и соединяем их. Стороны построенных треугольников пропорциональны сторонам исходного, а углы между ними равны углу ∆ АВС.

Смотрите на рисунок ...
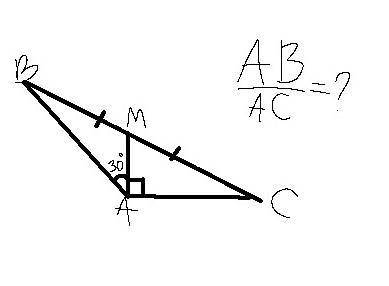
У сторон АВ и АС общая вершина - А, и через неё и проведём медиану АМ к стороне ВС ...
Будем искать:
АС/АВ = ?
ИЛИ
АВ/АС = ?
Итак ...
Что можно сказать про медиану?
Она делит треугольник на два треугольника, площади которых равны ...
Получаем :
1) Площадь треугольника АВМ = площадь треугольника АМС.Рассмотрим треугольник ВМА.
Его площадь можно найти по вот такой формуле:
Площадь треугольника ВМА = ½*АВ*АМ*синус угла ВАМ
По условию угол ВАМ равен 30° ...
Площадь треугольника ВМА = ½*АВ*АМ*синус угла в 30°
Синус в 30° равен ½.
Получаем:
Площадь треугольника ВМА = ¼*АВ*АМ.
Теперь посмотрим на треугольник АМС.
Он прямоугольный... А площадь прямоугольного треугольника равна половине произведения его катетов. (В нашем случае АМ и АС - катеты).
Запишем вот так :
Площадь треугольника АМС = ½*АС*АМ..
ПО ВЫШЕ СКАЗАННОМУ В ПУНКТЕ 1 СЛЕДУЕТ, ЧТО :
½*АВ*АМ = ¼*АМ*АС
½*АВ = ¼*АС
АВ = ½*АС ...
Получаем :
АС/АВ = АС/(½*АС) = 1 : ½ = 2.
АВ/АС = (½*АС)/АС = ½.
(ЕСЛИ НЕВЕРНО ОТМЕТЬТЕ КАК НАРУШЕНИЕ!)
Угол ВАД=30 градусов, МК - средняя линия, МК=5
Найти площадь АВСД.
Проведем высоту ВН, рассмотрим треугольник АВН - прямоугольный, угол А=30 градусов, тогда ВН=2 (как катет, лежащий против угла 30 градусов)
S=MK*BH=2*5=10 ед²