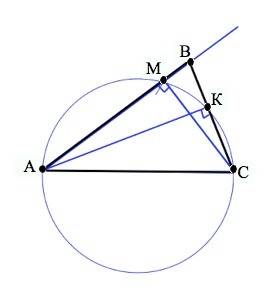
Пусть заданы отрезки: АС - сторона треугольника, АК и СМ - его высоты.. Требуется построить треугольник по данным элементам. • 1) На произвольной прямой откладываем отрезок АС, равный данной стороне. • 2) По известному методу деления отрезка пополам находим середину О отрезка АС и из О радиусом, равным АО, чертится окружность. • 3) Из А на построенной окружности отмечаем циркулем точку К ( длина АК равна длине одной из данных высот). Из точки С таким же образом на окружности отмечаем основание М второй высоты. • 4) Из точки А через М проводим прямую, из точки С через К проводим вторую прямую. Точку пересечения этих прямых обозначим В. Треугольник по стороне АС и высотам АК и СМ построен: Длина АС задана условием. Углы АКС и СМА прямые - опираются на АС как на диаметр окружности. Следовательно, АК - высота к ВС, СМ - высота к АВ.
L = 2πR. отсюда R = L/(2π) = 18π/(2π) = 9 см.
По радиусу находим сторону а вписанного равностороннего треугольника:
а = R√3 = 9√3 см.
Площадь S равностороннего треугольника , вписанного в эту окружность, определяем по формуле S = a²√3/4 = 273√3/4 см².