1 - периметр это сумма длин всех сторон. в равностороннем треуг. все стороны одинак стало быть 24 делим на 3 = 8 2 итак, в равнобедренном треуг только две стороны равны. нужно вычислить третью, которая является в равнобедренном основанием надо 80 - 30 -30 = 20. то есть если стороны равны 30 м, то основание 20 3 здесь наоборот известно основание. для того чтобы определить что осталось на две боковые стороны нужно вычесть из 80 длину основания 40м. получилось 40. но это две стороны вместе, а нам нужна одна. поэтому 40 делим на 2 = 20 м одна сторона 4. с этим придется порисовать чуток. итак, известно что ек это медиана (такой отрезок, который соединяет угол с СЕРЕДИНОЙ противоположной стороны). есть такое правило, которое говорит нам о том что в равнобедренном треугольнике медиана является и бисскетрисой (делит угол ПОПОЛАМ) и высотой (то есть когда из угла к стороне проведен отрезок под углом 90 градусов) и в любой последовательности. суть не меняется. так вот исходя из этого правила я воспользовавшись тем что ек это биссектриса могу с уверенностью сказать, что угол кес равен 44 градусам, так как известно что полностью угол е равен 88 градусов, а биссектриса ек делит его пополам. на всякий случай проверим. Сумма всех углов треугольника = 180 градусов. а углы при основании равнобедренного треугольника равны. проверяем 46+46+88 = 180. или по другому, если рассматривать треугольник екд, то 180 - 90-46-44 = 0. все верно
1) треугольник АВD - равносторонний ⇒ сторона АВ=АD АС - общая сторона для треугольников BAC и DAC угол ВАС = углу САD (т.к. АС биссектриса , которая делит ВАD пополам) ⇒ по 1 признаку равенства треугольников (по двум сторона и углу между ними) треугольник BAC = треугольнику DAC
3) т.к. МD= DК ⇒ ND - медиана, а т.к. ND ещё и высота ⇒ Δ МNК - равнобедренный ⇒ МN= КN МD= DК ND - общая для ΔMDN и ΔKDN ⇒ΔMDN = ΔKDN по 3 признаку (по трем сторонам)
Дана трапеция ABCD, BC║AD, AB=CD, BC=8см, AD=14см, S(ABCD)=44см².
Найти P(ABCD).
Пусть CM⊥AD, BN⊥AD и M,N∈AD.
Площадь трапеции равна произведению средней линии и высоты опущенной на основание.
S(ABCD) =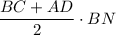 = BN·(8см+14см):2 = BN·11см = 44см²
= BN·(8см+14см):2 = BN·11см = 44см²
BN = 44:11 см = 4см
ΔABN = ΔDCM по гипотенузе и острому углу (AB=DC и ∠BAN=∠CDM т.к. трапеция равнобедренная), поэтому AN=MD
NBCM - прямоугольник, поэтому NM=BC=8см
AN = (AD-NM):2 = (14см-8см):2 = 3см
В прямоугольном ΔABN (∠N=90°): BN=4см и AN=3см, по Египетскому треугольнику AB=5см.
CD=AB=5см
P(ABCD) = AB+BC+CD+AD = 5см+8см+5см+14см = 32см
ответ: 32см.