1.площадь прямоугольника 120, ширина 8. найдите длину прямоугольника. 2.гипотенуза в треугольнике 10, катет 6. найдите второй катет. 3. могут ли боковые стороны прямоугольной трапеции, быть равными. 4. углы треугольника относятся как 3: 4: 5. вычислите их. , нужно . 25

👇

Ответ:

kravts222p08eoo

21.06.2021

1)Площадь=120
Ширина=8
Найдём через площадь высоту
Площадь прямоугольника равна a*b
120=x*8
120=8x
X=15
ответ:15
2)Катет можно найти по теореме Пифагора.
Теорема Пифагора-c^2=a^2+b^2 ( буквы может не те, как в теорем, но суть одна),
Но в данном случае ты ищешь не гипотенузу, а катет, а значит не складываешь a^2 и b^2, а вычитаешь
10^2-6^2= 100-36=64. Корень из 64=8
ответ:8
Надеюсь так)

4,8(63 оценок)

Открыть все ответы

Ответ:

Клава11111

21.06.2021

ответ: б) AB = 18 см, AC = 6 см в) AC = 33 см

Объяснение:

б) BC = BP + CP = 18 см

Обозначим две другие стороны Δ через x = AB и y = AC.

Из того, что периметр равен 42 получим:

x + y + 18 =42 ⇒ x + y = 24 (1)

Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒

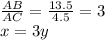
$\frac{AB}{AC}=\frac{13.5}{4.5}=3\\x=3y$

Подставим последнее равенство в (1) и получим:

4y = 24

y = 6

Тогда x = 18

в) Обозначим x = AC. Т.к. BE медиана, то AE = CE = x/2, AD = x/2 - 4.5, CD = x\2 +4.5

Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒

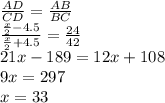
$\frac{AD}{CD}=\frac{AB}{BC}\\\frac{\frac{x}{2}-4.5}{\frac{x}{2}+4.5}=\frac{24}{42}\\21x-189=12x+108\\9x=297\\x=33$

4,6(86 оценок)

Ответ:

nastyusha19032002

21.06.2021

(-2,2; -0,6)

Объяснение:

Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:

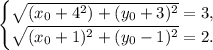
$\begin{cases}\sqrt{(x_0+4^2)+(y_0+3)^2}=3,\\\sqrt{(x_0+1)^2+(y_0-1)^2}=2.\end{cases}$

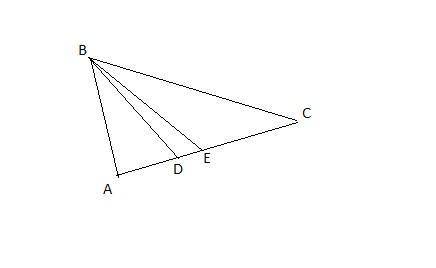
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.

Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно 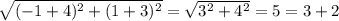$\sqrt{(-1+4)^2+(1+3)^2}=\sqrt{3^2+4^2}=5=3+2$ . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо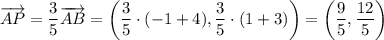 $\overrightarrow{AP}=\dfrac{3}{5}\overrightarrow{AB}=\left(\dfrac{3}{5}\cdot(-1+4),\dfrac{3}{5}\cdot(1+3)\right)=\left(\dfrac{9}{5},\dfrac{12}{5}\right)$

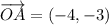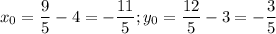Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор $\overrightarrow{OA}=(-4,-3)$ , мы получим координаты точки P(x₀, y₀): $x_0=\dfrac{9}{5}-4=-\dfrac{11}{5}; y_0=\dfrac{12}{5}-3=-\dfrac{3}{5}$ .