Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы.
По т.Пифагора с²=a²+b², где с - гипотенуза, a и b – катеты.
с=√(9²+12²)=15
R=15:2=7,5 см
Подробно.
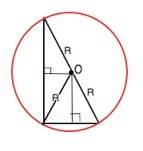
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров к его сторонам.
Срединные перпендикуляры прямоугольного треугольника пересекаются на середине гипотенузы, следовательно центр описанной окружности - середина гипотенузы, и радиус описанной окружности прямоугольного треугольника равен половине гипотенузы. R=7,5 см.
1,8 < b < 1,9
минимальное значение c
c > min(a) - max(b)
c > 2,3 - 1,9
с > 0,4
максимальное значение c
c < max(a) + max(b)
c < 2,4 + 1,9
с < 4,3
0,4 < с < 4,3