8+16√2 см²
Объяснение:
Дано:
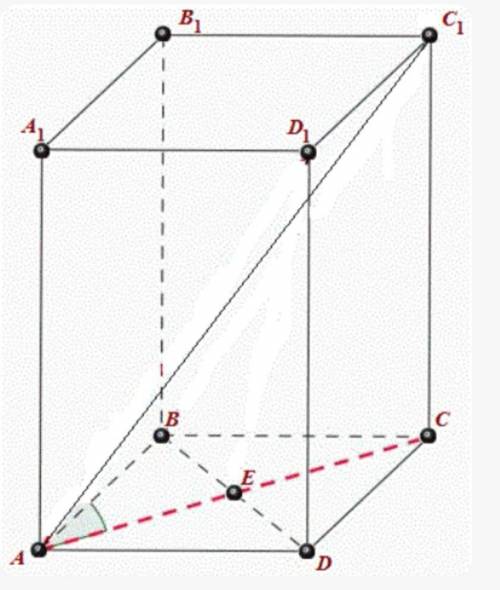
АВСDA1B1C1D1 призма.
АВСD- квадрат.
АС1=4см диагональ призмы.
АВ=ВС=СD=AD=2см
Sпол=?
Решение
Sпол=2Sосн+Sбок
Sосн=АВ²=2²=4 см² площадь квадрата.
АС- диагональ квадрата.
АС=АВ√2=2√2 см диагональ квадрата.
∆АС1С- прямоугольный.
АС1- гипотенуза.
АС и СС1 - катеты.
По теореме Пифагора найдем СС1
СС1=√(АС1²-АС²)=√(4²-(2√2)²)=√(16-8)=√8=
=2√2 см высота призмы.
Формула нахождения площади боковой поверхности призмы
Sбок=Росн.*h, где Росн.-периметр основания (квадрата); h=CC1.
Sбок=4*АВ*СС1=4*2*2√2=16√2 см² площадь боковой поверхности призмы.
Sпол.=2*Sосн.+Sбок=2*4+16√2=8+16√2 см² площадь полной поверхности призмы.
Имеем равносторонний треугольник ОАС, в котором все углы по 60 градусов, значит, угол АОС=60 градусов и дуга АС=60 градусов.
Треугольник АВС - равнобедренный, значит дуга ВС=дуге АВ
дуга ВС+дуга АВ=360-60=300 градусов
Дуга АВ=дуге ВС=300:2=150 градусов.
ответ: 60 градусов, 150 градусов, 150 градусов.