Объяснение:
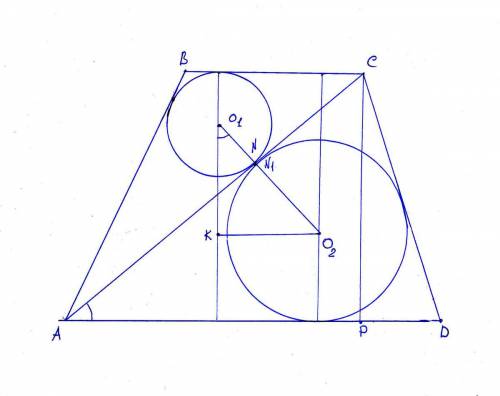
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.
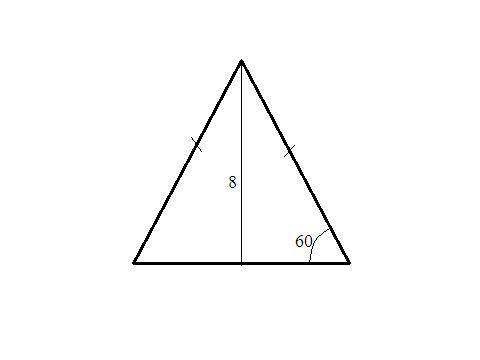
угол CAB = 60
т.к. напротив угла в 30 градусов лежит катет в два раза меньше гипотенузы.
высота и есть этот катет. а так как угол C1BC 30 градусов, то следовательно угол CAB 60