точка пересечения хорд - это гипотенуза в прямоугольном треугольнике с катетами, равными расстояниям от хорд до центра окружности.
то есть по теореме Пифагора можно найти искомое расстояние от центра окружности до точки пересечения хорд:
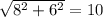
А) Сумма острых углов в прямоугольном треугольнике = 90°.
Пусть один угол из них = х, тогда второй острый угол = 90° - х
б) сумма внешних углов = 180°
Для угла = х внешний угол = 180° -х
для другого угла внешний угол = 180° -(90° -х) = 180° - 90° +х= 90° +х
в) (180° - х)/(90° +х) =12/15
(180° - х)/(90° +х) =4/5
5(180° - х) = 4(90° +х)
900 - 5х = 360 + 4х
9х = 540
х = 60° ( это один острый угол данного прямоугольного треугольника)
90° - 60° = 30°( это второй острый угол)
ответ: 60° и 30°
здесь главное-правильно нарисовать рисунок.
при пересечении хорд и проведении расстояний до центра окружности получится прямоугольник со сторонами 6 и 8 см. Расстояние от точки пересечения до центра - есть диагональ этого прямоугольника. Теперь рассмотрим один прямоугольный треугольник в этом прямоугольнике, где расстояние в квадрате = 6 в квадрате+8 в квадрате=36+64=100
расстояние = 10.