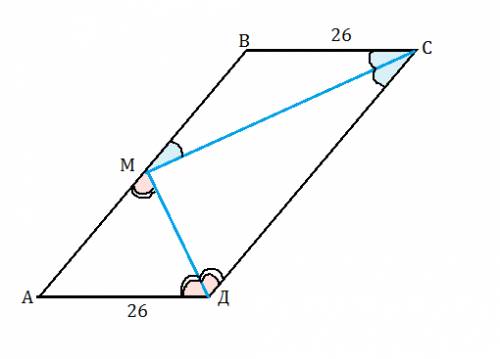
Точка пересечения биссектрисс делит противоположную сторону на два отрезка, каждый из которых вместе с соседней боковой стороной и самой биссектриссой образует треугольник. Оба эти треугольника - равнобедренные, поскольку угол, который биссектриса образует с противоположной стороной, является внутренним накрест лежащим для одного из двух равных углов, на которые она - биссектриса - делит угол параллелограмма.
Поэтому оба треугольника равнобедренные, и оба отрезка противоположной стороны равны соседним боковым сторонам.
То есть большая сторона равна 26 + 26 = 52
d1 · d2 = 24. d1=4 см; d2=6 см.
Диагонали делят ромб на 4 равных прямоугольных треугольника, катеты которых равны половине диагоналей d1 и d2.
d1=4/2=2 см; d2=6/2=3 см.
Найдем гипотенузу одного из прямоугольных треугольников, которая будет одновременно стороной ромба.
а²=2²+3²=4+9=13. Сторона ромба равна а=√13 см.