1. Сумма острых углов в прямоугольном треугольнике = 90°. Следовательно, угол А = 90-21=69°.
2. По свойству прямоугольного треугольника, угол ОЕВ = 45°. Треугольник равнобедренный, ОЕ=ОВ=34см.
3. Угол ЕСМ = 90°-60°=30°.
Катет ЕМ, лежащий против угла в 30 градусов = половине гипотенузы СМ. ЕМ = 42см.
4. Если сумма острых углов = 90°, то:
8х+7х=90°
15х=90°
х=6.
Следовательно, один из углов = 8×6=48°, второй = 7×6=42°.
5. Сумма острых углов в прямоугольном треугольнике= 90°.
Составим уравнение.
х+(х+42)=90
2х=48
х=24
Следовательно, один из углов = 24°, другой 24+42=66°.
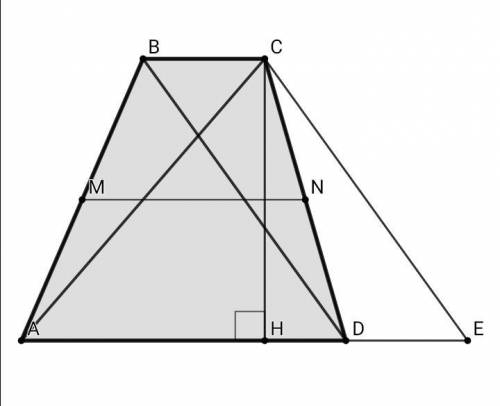
Выведу обобщённую формулу для подобных задач про трапецию с известными диагоналями AC = x, BD = y, и суммой оснований BC + AD = m
Проведём из вершинны С прямую СЕ, параллельную BD, тогда BC || DE, CE || BD ⇒ BCED - параллелограми, ВС = DE, CE = BD = y
S (abcd) = (BC + AD)•CH/2 = (DE + AD)•CH/2 = AE•CH/2 = S (ace)
Площадь трапеции ABCD равна площади треугольника ACE
Найдём плошадь ΔАСЕ по формуле Герона: АС = х, CE = y, AE = m
Площадь трапеции с диагоналями х и у и суммой оснований равной m:S = √( p • (p - x) • (p - y) • (p - m) ) , где р = (х + y + m)/2Средняя линия трапеции: MN = (BC + AD)/2 = 5 ⇒ m = 10, x = 9, у = 17
S (abcd) = √(18•(18 - 9)(18 - 17)(18 - 10)) = √(18•9•1•8) = 36ответ: 36
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
Если что неясно - спроси