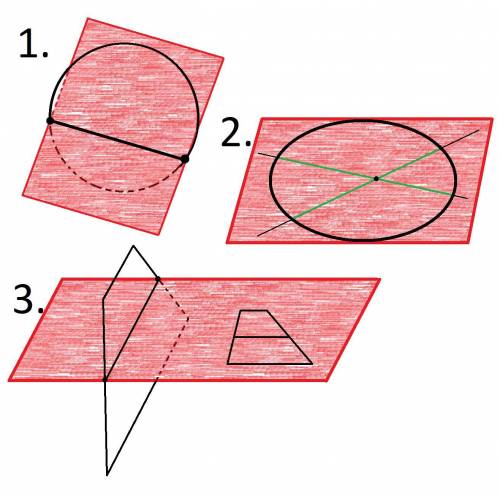
1.
Нет, неверно.
Окружность не всегда, но может пересекать эту плоскость.
2.
Да, верно.
Окружность лежит в данной плоскости т.к. две пересекающие прямые (содержащие хорды, которые пересекаются), принадлежащие плоскости окружности, содержатся в данной плоскости. А значит любая точка окружности так же принадлежит данной плоскости.
3.
Нет, не пересекает.
Средняя линия параллельна основаниям. Поэтому основания либо параллельно данной плоскости (по признаку параллельности прямой и плоскости), либо лежит в этой плоскости (ведь для параллельных прямых существует плоскость, в которой они лежат). Среди возможны взаимных расположений прямой и плоскости нету такого, что прямая будет пересекать плоскость.
Углы при основаниях равны
∠ОВА = (180 - 50)/2 = 65°
∠ОВС = (180 - 140)/2 = 20°
Далее возможны два варианта, в зависимости от того, в одном направлении отсчитываются углы дуг АВ и ВС или в противоположных
1. В одном направлении
∠АОС₁ = 360 - 50 - 140 = 170°
∠АВС₁ = 65 + 20 = 85°
2. В противоположных направлениях
∠АОС₂ = 140 - 50 = 90°
∠АВС₂ = 65 - 20 = 45°