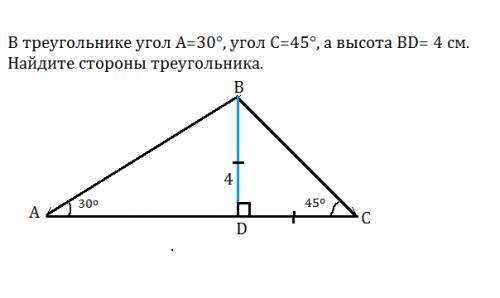
В треугольнике угол A=30° угол C=45° а высота BD= 4 см.
Найдите стороны треугольника.
----------------------
Высота ВД противолежит углу, равному 30º. ⇒ BD равна половине гипотенузы ∆ АВД.
Гипотенуза АВ=4*2=8 см.
АD найдем по т.Пифагора:
АD²=АВ²-ВD²
АD=√(64-16)=√48
АD=4√3 см
В прямоугольном ∆ ВDС острый угол ВСD=45º, ⇒ угол СВD=45º,
∆ СВD - равнобедренный, СD=ВD=4 см
По т.Пифагора ВС=4√2 см ( проверьте)
Тогда АС=АD+DС=4√3+4=4(√3+1)
Стороны равны
АВ=8,
ВС=4√2
AC =4(√3+1)
-----------
Если Вы уже изучали тригонометрические функции, то можно использовать их значение для заданных углов.
АВ=ВD:sin30º=4:0,5=8 см
BC=BD:sin45º=4:(√2)/2=4√2 см
АС=АD+DС=4√3+4=4(√3+1) см
1.
(n-2)*180"
если n=6, тогда:
(6-2)*180" = 4*180 = 720
720/6= 120 градуса
если n=10, тогда:
(10-2)*180" = 8*180 = 1440
1440/10=144 градуса
2.
Если n-число сторон и углов, то сумма всех углов 135n
Сумма углов n-угольника находится по формуле 180(n-2)
приравниваем эти выражения, решаем уравнение:
135n=180(n-2)
135n=180n-360
45n=360, отсюда n=8
150n=180(n-2)
150n=180n-360
30n=360, отсюда n=12