Площадь полученного шестиугольника будет меньше площади данного шестиугольника на шесть площадей равных равнобедренных треугольников. У этих треугольников боковые стороны равны ½ стороны данного шестиугольника, а угол между ними равен 120⁰.
SΔ= ½ ab · sin γ
S = ½ · ¼a² · (√3)/2 =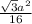 
(кв.ед.)
Из формулы площади шестиугольника S=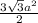
выражаем сторону а:
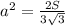
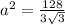
Подставляя в формулу площади треугольника, находим, что SΔ = 8/3 кв.ед.
6SΔ = 16 кв.ед.
Площадь полученного шестиугольника равна 64-16=48 (кв.ед.)
Из прямоугольного треугольника ABD
AD^2=AB^2+BD^2=9+16=25
AD=5
Площадь основания равна 2*площадь ABD=2*(3*4/2)=3*4=12
AD параллельно BC, следовательно параллельно B1C1, поэтому AD принадлежит плоскости AB1C1, и это прямая пересечения плоскости основания с плоскостью AB1C1
Пусть BE высота в треугольнике ABD
Тогда угол B1EB это угол между плоскостью основания и плоскостью AB1C1, так как BE перпендикулярно AD, B1E перпендикулярно AD по теореме о трёх перпендикулярах.
Треугольник B1EB -- прямоугольный треугольник с углом 45 градусов, а следовательно, равнобедренный прямоугольный треугольник, поэтому B1B=BE
Чтобы найти высоту BE выразим площадь треугольника ABD двумя
площадь ABD = AB*BD/2 = AD*BE/2, отсюда
BE=AB*BD/AD=3*4/5=12/5=2,4
Площадь полной поверхности равна
2*площадь основания+площадь боковой поверхности
площадь боковой поверхности = периметр основания умножить на высоту
периметр основания = AB+BC+CD+AD=3+5+3+5=16
тогда площадь боковой поверхности 16*2,4=38,4
площадь полной поверхности
2*12+38,4=24+38,4=62,4
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности: S = p*r
где p = 1/2(a+b+c) - полупериметр
Есть и еще одна формула, применяемая в основном в задачах части C:
S = abc/4R - R - радиус описанной окружности.
Так же для треугольника с описанной окружностью работает теорема синусов (рис.2)
Теперь по многоугольникам
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Теорема Птолемея. Произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон.
Квадрат.Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Прямоугольник. Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Трапеция. Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
_______________
Если есть вопросы - спрашивай, дополню