S = 14 ед.²
V = 3 ед.³
Объяснение:
Рассмотрим более простой по форме прямоугольный параллелепипед с длиной а=2, высотой h=2 и шириной b=1.
Площадь такой фигуры состоит из 4 равных боковых граней, размером 2х1 и равных фронтальной и тыльной граней, размером 2х2.
Тогда площадь S₁ всей фигуры равна: S₁ = 4*2*1 + 2*2*2 = 16 ед.²
Объём V₁ такой фигуры равен:
V₁ = a*b*h = 2*1*2 = 4 ед.³
Определим, на сколько меньше площадь S₂ и объём V₂ фигуры, данной в условии, площади S₁ и объёма V₁ прямоугольного параллелепипеда.
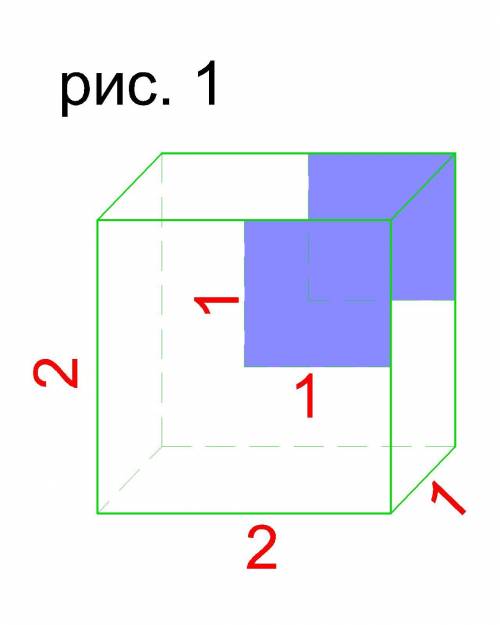
Рассмотрим Рисунок 1.
Из него видно, что S₂ меньше чем S₁ на 2 квадрата размером 1х1 ед.
Тогда S₂ = S₁ - 2*1*1 = 16-2 = 14 ед.²
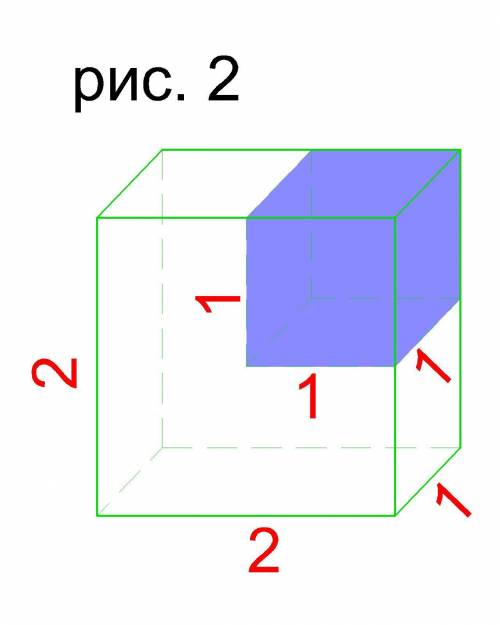
Рассмотрим Рисунок 2.
Из него видно, что V₂ меньше чем V₁ на куб размером 1х1х1 ед.
Тогда V₂ = V₁ - 1*1*1 = 4-1 = 3 ед.³
S = πd²/4 = 415
πd² = 1660
d = √(1660/π) см
Теорема косинусов для осевого сечения
d² = 2l² - 2l²cos(74°)
d² = l²(2 - 2cos(74°))
l = d/√(2 - 2cos(74°))
Образующая
l = √(1660/π)/√(2 - 2cos(74°)) = √(830/(π(1 - cos(74°))) ≈ 19.1 см
Площадь осевого сечения
S = 1/2*l²*sin(74°) = 415*sin(74°)/(π(1 - cos(74°)) ≈ 175.3 см²