Периметр сечения равен 19 см.
Объяснение:
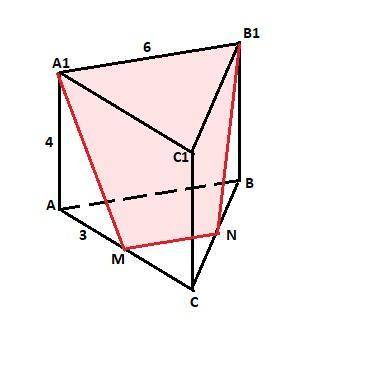
Пусть дана правильная треугольная призма АВСА1В1С1. Сечение, проходящее через ребро A1B1 и точку M - середину AC - равнобедренная трапеция А1В1NM, где точка N - пересечение стороны ВС основания с прямой МN - параллельной А1В1 (а значит и параллельной стороне АВ), так как параллельные грани АВС и А1В1С1 пересекаются плоскостью сечения по параллельным прямым.
В треугольнике АВС MN - средняя линия и равна половине стороны АВ, то есть MN= 3 см.
Боковые стороны трапеции найдем из прямоугольного треугольника АА1М с катетами, равными 4 см и 3 см (точка М - середина стороны АС).
Это Пифагоров треугольник. А1М = 5 см.
Периметр сечения равен 6+2·5+3 = 19 см.
Периметр сечения равен 19 см.
Объяснение:
Пусть дана правильная треугольная призма АВСА1В1С1. Сечение, проходящее через ребро A1B1 и точку M - середину AC - равнобедренная трапеция А1В1NM, где точка N - пересечение стороны ВС основания с прямой МN - параллельной А1В1 (а значит и параллельной стороне АВ), так как параллельные грани АВС и А1В1С1 пересекаются плоскостью сечения по параллельным прямым.
В треугольнике АВС MN - средняя линия и равна половине стороны АВ, то есть MN= 3 см.
Боковые стороны трапеции найдем из прямоугольного треугольника АА1М с катетами, равными 4 см и 3 см (точка М - середина стороны АС).
Это Пифагоров треугольник. А1М = 5 см.
Периметр сечения равен 6+2·5+3 = 19 см.

с = 4 и 6 см
катеты состоят тоже из двух отрезков каждый, и их длины равны
a = 4 + r см
b = 6 + r см
Теорема Пифагора
c² = a² + b²
10² = (4 + r)² + (6 + r)²
100 = 16 + 8r + r² + 36 + 12r + r²
2r² + 20r + 52 - 100 = 0
2r² + 20r - 48 = 0
r² + 10r - 24 = 0
Дискриминант
D = 10² + 4*24 = 196 = 14²
r₁ = (-10 + 14) / 2 = 2 см
r₂ = (-10 - 14) / 2 = -12 см - отбрасываем
---
катеты
a = 4 + r = 6 см
b = 6 + r = 8 см
Площадь большого треугольника
S = 1/2*ab = 1/2*6*8 = 24 см²