2. Сумма углов восьмиугольника вычисляется по формуле: 
. Разделив это число на 8, найдем чему равен один угол. 
. По определению, внешний угол это угол, смежный с любым внутренним. А так как сумма смежных углов равна 180 градусам, получаем: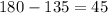 
, что и сходится с утверждением.
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.
x = 0
y + 3 = 0
y = - 3
А(0; -3)
---
y = 0
3/4*x + 3 = 0
3x + 12 = 0
x + 4 = 0
x = - 4
B(-4; 0)
---
Треугольник АОВ прямоугольный
Длины катетов треугольника
ОА = 3
ОВ = 4
Гипотенуза по т. Пифагора
АВ = √(3² + 4²) = √(9+16) = √25 = 5
---
Диаметр описанной вокруг прямоугольного треугольника окружности равен гипотенузе
d = 5
Площадь
S = πr² = πd²/4
S = π*5²/4 = 25π/4