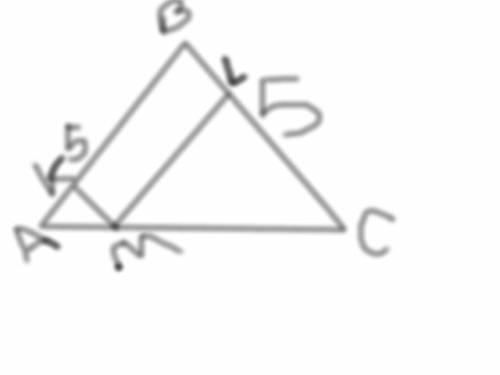

ответ: 9 см и 23 см
Пусть трапеция АВСD, а ВК - биссектрисса тупого угла АВС. Поскольку она параллельна боковой стороне СD, то ВСDК - параллелограмм
Угол СDК равен углу АВК т.к. ВК - биссектриса.
Угол СDК равен углу КВС как противолежащие углы параллелограмма.
Угол СDК равен углу А, как углы при основании равнобокой трапеции. Следовательно, угол АВС равен двум углам А, и угол А + угол АВС =180° отсюда угол А = 60°, угол АВК = 60° и треугольник АВК - равносторонний АВ = АК = BK = 14, значит ВС + КD = 60 - (14*3) = 18. ВС = 18 : 2 = 9 см
АD = 9 + 14 = 23 см.
∠АВО = ∠СВО по условию
ВО - общий катет
Следовательно, ΔАВО = ΔСВО по катету и прилежащему острому углу.
В равных треугольниках соответствующие элементы равны, отсюда:
АО = СО
Рассмотрим треугольник АDС:
DО ⊥ АС (по условию) ⇒ DО - высота
АО = СО (доказано выше) ⇒ DО - медиана
Если DО является медианой и высотой, тогда ΔАDС - равнобедренный, с основанием АС, отсюда:
АD = DС, что и требовалось доказать.