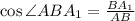 ; С другой
; С другой 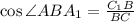 ; Получаем
; Получаем 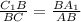 , Значит треугольники C₁BA₁ и ABC подобны по общему углу ABA₁ и двум пропорциональным сторонам, причем коэффициент подобия равен косинусу общего угла. Найдем косинус угла по теореме косинусов.
, Значит треугольники C₁BA₁ и ABC подобны по общему углу ABA₁ и двум пропорциональным сторонам, причем коэффициент подобия равен косинусу общего угла. Найдем косинус угла по теореме косинусов.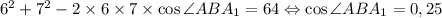 ; Поэтому
; Поэтому 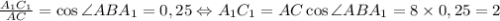 ; Отсюда
; Отсюда 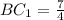 ;
; 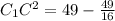 ;
; 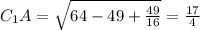 ; Треугольники C₁AH и A₁HC подобны по двум углам.
; Треугольники C₁AH и A₁HC подобны по двум углам. 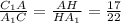 ; При этом
; При этом 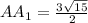 ; Значит
; Значит 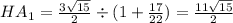 , откуда
, откуда 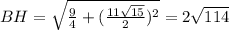
См. Объяснение
Объяснение:
Задание
Прочти высказывания и оцени их верность.
1) Площадь параллелограмма равна полусумме его оснований —
2) Высота прямоугольного треугольника равна корню из разности квадрата его гипотенузы и квадрата его второго катета —
3) Площадь квадрата равна квадрату его высоты —
4) Высота трапеции равна её площади, делённой на среднюю линию —
Решение
1) "Площадь параллелограмма равна полусумме его оснований" — неправильно; площадь параллелограмма равна произведению одной из его сторон на высоту, проведённую к этой стороне.
2) "Высота прямоугольного треугольника равна корню из разности квадрата его гипотенузы и квадрата его второго катета" — в данном случае приведена формула вычисления одного из катетов; если принять один из катетов за основание, а второй за высоту, то, в частности, с этим утверждением можно было бы согласиться, но ведь кроме катетов в треугольнике есть ещё и гипотенуза, высота к которой проводится из вершины прямого угла, и в отношении высоты, проведенной к гипотенузе, такая формула неприменима; поэтому ответ - неправильно.
3) "Площадь квадрата равна квадрату его высоты" — площадь квадрата равна квадрату его стороны, а понятия "высоты квадрата" нет; ответ - неправильно.
4) "Высота трапеции равна её площади, делённой на среднюю линию" - да, так можно утверждать; если площадь трапеции равна произведению средней линии на высоту, то из этого следует, что делением площади на среднюю линию мы получаем высоту трапеции; ответ - правильно.
Ответ: 6 см
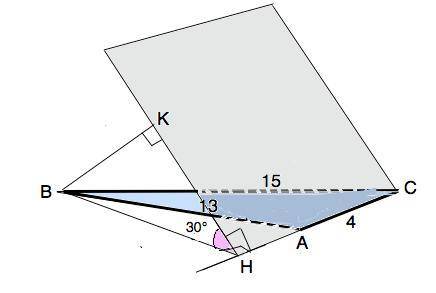
Объяснение: Угол между плоскостями — это угол между перпендикулярами, проведенными в этих плоскостях к одной точке на линии их пересечения.
Линия пересечения - прямая СА, перпендикуляры к ней НВ и НК. Угол ВНК=30°(дано)
ВН - высота ∆ АВС к стороне АС. Площадь ∆ АВС по формуле Герона равна 24 см².
Из формулы площади треугольника высота ВН=2Ѕ:АС=48:4=12 (см).
Расстояние от точки до плоскости измеряется длиной перпендикуляра, опущенного из той точки на плоскость.
Из прямоугольного ∆ ВКН искомое расстояние ВК=ВН•sin30°=12•1/2=6 см