Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
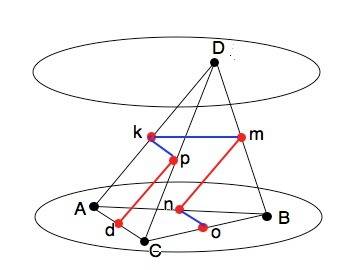
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
К-вершина
М-середина АС
КМ-апофема
треугольник КМО-прямоугольный
КМ=КО*2=2*2=4 теорема об угле 30°
МО=r
МО=√КМ²-КО²=√4²-2²=√16-4=√12=2√3
r=a/2√3
a=2√3*2√3=12
Sб п=1/2Росн*L
L-апофема
Sб п=1/2*36*4=72