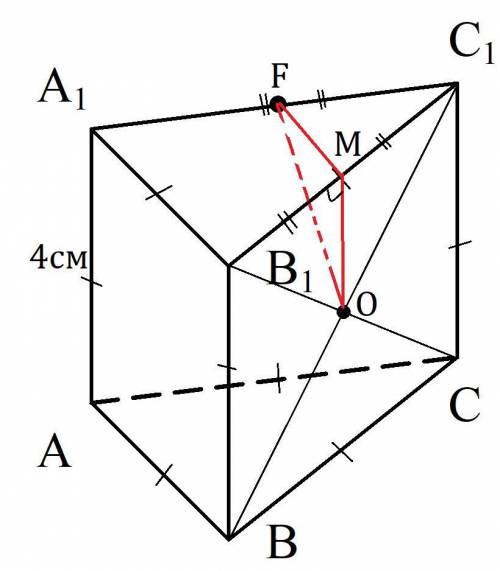
Дано: ABCA₁B₁C₁ - прямая призма с равными рёбрами. F∈A₁C₁; A₁F = FC₁
BC₁∩CB₁ = O
Найти: FO.
Боковые грани призмы это квадраты т.к. рёбра равны и призма прямая.
Пусть M∈B₁C₁ и OM⊥B₁C₁ тогда OM - медиана (т.к. ΔB₁O₁C₁ - равнобедренный), то есть B₁M = MC₁ значит FM - средняя линия ΔA₁C₁B₁.
FM = A₁B₁:2 = 4:2 см = 2см - как средняя линия.
MO = MB₁ - как катет в прямоугольном Δ с острым углом в 45° (ΔB₁OM).
MO = B₁C₁:2 = 4:2 см = 2см.
FM ⊥ MO т.к. призма прямая, то есть линейный угол, двугранного угла между основаниями и боковыми гранями, будет 90°.
По теореме Пифагора в прямоугольном ΔFMO:
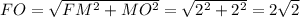 см.
см.
ответ: 2√2 см.
В прямоугольном треугольнике, образованном высотой и стороной параллелограмма как гипотенузой, острый угол против высоты является смежным с тупым углом параллелограмма. В параллелограмме угол между высотами из вершины острого угла равен тупому углу, 150°. Следовательно, смежный с ним угол равен 180°-150°=30°. Катет против угла 30° равен половине гипотенузы, высоты равны половинам сторон параллелограмма, стороны равны 6 и 4. В параллелограмме сумма квадратов диагоналей равна сумме квадратов четырех сторон, 2(36+16)=104.