48
Объяснение:
Продолжим боковые стороны трапеции (О - точка пересечения). Пусть OB = a, OC = b. В треугольнике AOD биссектриса делит сторону AO так, что 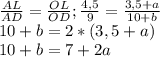
Поскольку в треугольнике AOD отрезок BC параллелен основанию AD (как основания трапеции), справедливо равенство:
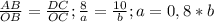
Подставляем полученное выражение в найденное ранее:
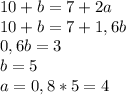
То есть, ОВ = 4 и ОС = 5. Тогда имеем треугольник AOD со сторонами 9, 12 и 15 см => треугольник прямоугольный (подчиняется теореме Пифагора), и угол между сторонами AD и AB равен 90 градусов, и следовательно угол B также будет прямым.
Основание BC можно найти как катет в прямоугольном треугольнике OBC с катетом 4 и гипотенузой 5, оно будет равно 3 (по теореме Пифагора). В таком случае площадь трапеции равна произведению полусуммы оснований на высоту, т.е. 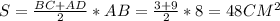
Я вроде бы это уже доказывал тебе, докажу еще раз.
Центр вписанной окружности находится в точке пересечения биссектрис, т.к. центр описанной окружности лежит на медиане, от одна из медиан совпадает с биссектрисой, иначе медиана пересекает биссектрису в 2 точках, а это невозможно. А т.к. совпадают медиана и биссектриса, то треугольник равнобедренный