Доказательство:
Так как треугольник остроугольный и BD - биссектриса, то ∠B<90°⇒∠CBD<45°=∠DFC, следовательно F∈BC.
Проведем из точки D перпендикуляр до отрезка BC с основанием M, M будет принадлежать стороне BC поскольку треугольник остроугольный.
Тогда прямоугольные треугольники BDE и BDM равны по общей гипотенузе BD и острым углам ∠DBE, ∠DBM. Из этого следует что, 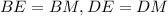 .
.
Также из-за того что, ∠DBC<∠DFC=45°<∠DMC=90°⇒F∈BM, теперь можно пользоваться тем что 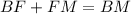 .
.
Заметим что, DFM - прямоугольный треугольник с углом 45°, то есть 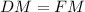 .
.
Учитывая доказанные равенства получаем,
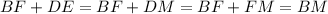
Что требовалось доказать.
Объяснение:
Окружность с центром в точке А и радиусом 3 см имеет с прямой BС две общие точки. Не верно.
Поскольку прямая расстояние от центра окружности А до стороны ВС, больше радиуса окружности r<AC, r<AB, то прямая и окружность не имеют общих точек.
Окружность с центром в точке А и радиусом 8 см имеет с прямой ВС одну общую точку. Верно.
Если расстояние от центра окружности до прямой равно ее радиусу, то прямая и окружность имеют одну общую точку касания.
Окружность с центром в точке В и радиусом 17 см имеет с прямой АС две общие точки. Не верно
Поскольку радиус окружность равен гипотенузе r=AB, то А∈окружности. Остальные точки АС не имеют с окружностью общих точек, поскольку меньше радиуса окружности.
Окружность с центром в точке В и радиусом 9 см имеет с прямой AС одну общую точку. НЕ ВЕРНО
Поскольку расстояние от точки В до АС от 15 см до 17 см, то окружность с АС не имеет общих точек.
В приложении есть рисунки для демонстрации утверждений.
Подробнее - на -
Решение на рисунке.
***************