1) 330√2 м³
2) arccos(5/√299)
Объяснение:
1.Основание любого параллелепипеда это параллелограмм, площадь которого вычисляется как произведение двух его сторон на синус угла между ними.
Sосн=6·11·sin45°=33√2 м²
Объём прямого параллелепипеда равен произведению бокового ребра(равен высоте) на площадь основания.
V=10·33√2=330√2 м³
2.Боковые грани правильной четырехугольной пирамиды равнобедренные и равные между собой 4 треугольника, ортогональные проекции которых вместе образуют основание пирамиды. А основание квадрат
Найдём боковую площадь данной пирамиды, которая в 4 раза больше чем площадь одной боковой грани.
По Герону p=0,5(9+9+5)=11,5
S²=p(p-5)(p-9)(p-9)=11,5·6,5·2,5²
(4S)²=16S²=16·11,5·6,5·2,5²=23·13·5²=299·5²
Sбок=4S=5√299
Sосн=5²=25
Пусть угол наклона боковой грани пирамиды к основанию равен α
Sосн=Sбок·cosα⇒cosα=Sосн/Sбок=25/(5√299)=5/√299≈0,0167
α=arccos(5/√299)
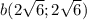 или
или 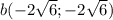
В пространстве (4; 4; 4) или (-4; -4; -4)
Объяснение:
Пусть вектор b имеет координаты (x; y). Так как координаты по условию равны, то можно записать b(x; x).
Модуль вектора - это его длина, которую находят по формуле: квадратный корень из суммы квадратов координат, что записывается так:
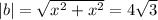
Решаем уравнение относительно x:
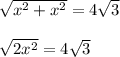
Возводим обе части уравнения в квадрат:
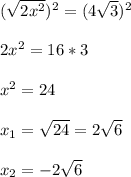
Значит координаты вектора 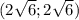 или
или 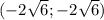
P.S. Если вектор в пространстве, то он имеет 3 координаты, тогда уравнение имеет вид:
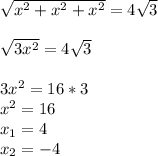
Значит вектор имеет координаты (4; 4; 4) или (-4; -4; -4)
ответ: ≈113
Объяснение:
№6.
Полная поверхность конуса:
S=3,14*rL+3,14*r² ( L- образующая конуса =5).
S (бок)-S(осн.)=4*3,14 ;
3,14*r*L-3,14*r²=4*3,14 ; (L=5)
Сразу сокращаем на 3,14 .
Получаем квадратное уравнение.
r²-5r+4=0.
r₁₂=(5±√25-16)/2;
r₁=(5+3)/2=8/2=4; r₂=(5-3)/2=1.
Этот корень не подходит, так как в условии r ≥ H. При проверке это подтверждается. Сама можешь проверить. Я проверила.
Находим полную поверхность конуса:
S=3,14*4*5+3,14*4²=3,14(4*5+16)=3,14*36=113,04≈113.