Основание прямой призмы — ромб с острым углом 45°, высота призмы равна 15 см. Цилиндр с боковой поверхностью 90π см² вписан в призму. Определи площадь боковой поверхности призмы.
Объяснение:
S(бок.призмы)=Р(осн)*h , где h-высота призмы. Высота призмы совпадает с высотой цилиндра.
Найдем сторонууууу ромба.
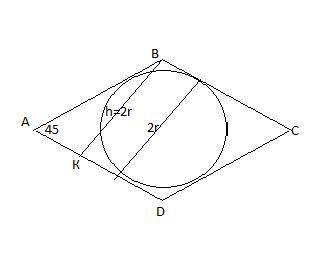
В основании призмы-ромб с вписанной окружностью (касается сторон ромба ). Высота ромба составляет 2r .
S(бок.цилиндра)=2π * r* h , или
90π=2π * r* 15 или r=3 см. Тогда высота ромба 6см.
Рассмотрим ΔАВК-прямоугольний , sin45°=ВК/АВ ,√2/2=6/АВ , АВ=6√2 см. Тогда Р(ромба)=4*6√2=24√2 (см)
S(бок.призмы)=24√2*15=360√2 (см²)
ответ:36 см^2
Объяснение:Пусть сторона основания равна а.
Тогда высота основания h = a*sqrt(3)/2
S = 1/2 *a*a*sqrt(3)/2 = 9*sqrt(3) => a = 6 см
Одно из боковых рёбер пирамиды перпендикулярно снованию.
Его длина M =h*tg(30) = h/sqrt(3) = 3 см
Два других равны между собой, их длины находим из условия:
N^2 =M^2 +a^2 => N = 3*sqrt(5) см
Площадь каждой из перпендикулярных боковых граней:
S1 = 1/2 *M*a = 9 см^2
Высота третьей боковой грани P = 2*N = 6 см
Её площадь S2 = 1/2 *a*P = 18 см^2
Площадь боковой поверхности пирамиды
Sбок = 2*S1 +S2 = 36 см^2
Всё понятно?
а) Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ⇒ ∠ВАЕ = ∠ВЕА = 40°
∠А = 2∠ВАЕ = 2 * 40 = 80° (так как АЕ - биссектриса ∠А)
Сумма соседних углов параллелограмма равна 180° ⇒
∠В = 180 - ∠А = 180 - 80 = 100°
Противоположные углы параллелограмма равны ⇒
∠С = ∠А = 80°
∠D = ∠В = 100°
ответ: 80°; 80°; 100°; 100°.
-------------------------------------------------------------------------
б) ΔKLH - прямоугольный ⇒ ∠К = 90 - 42 = 48°
Сумма соседних углов параллелограмма равна 180° ⇒
∠L = 180 - ∠K = 180 - 48 = 132°
Противоположные углы параллелограмма равны ⇒
∠M = ∠K = 48°
∠N = ∠L = 132°
ответ: 48°; 48°; 132°; 132°.