Площа трикутника дорівнює 432 см²
Объяснение:
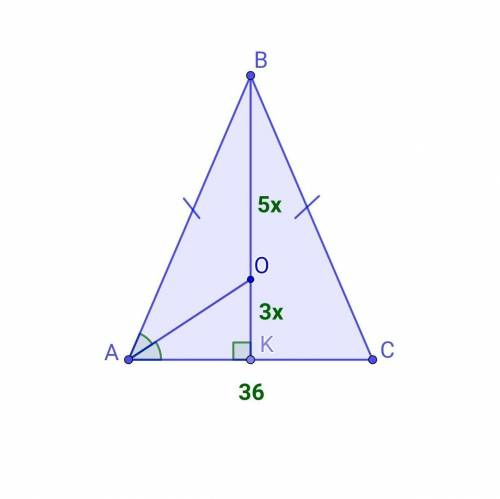
Обчислити площу рівнобедреного трикутника, якщо відомо, що бісектриса кута при основі ділить висоту, проведену до основи у відношенні 5:3, а основа трикутника - 36 см.
Розв'язанняНехай АВС - даний трикутник, АВ=ВС, ВК - висота, АО - бісектриса кута А, АС=36 см, ВО:ОК=5:3.
Знайдемо S(△АВС).
1) Так як ВК - висота, проведена до основи рівнобедреного трикутника, то ВК є медіаною (за властивістю), тому:
АК=КС=АС:2=36:2= 18 (см)
2) За властивістю бісектриси кута трикутника, у △АВК маємо:

Нехай ВО=5х, ОК=3х, де х - коефіцієнт пропорційності, тоді:
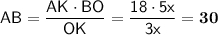 (см).
(см).
3) У прямокутному трикутнику АВК за теоремою Піфагора знайдемо катет ВК:
АВ²=ВК²+АК²
30²=ВК²+18²
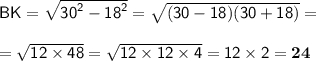
Отже, висота △АВС: ВК=24 (см)
4) Площу трикутника АВС знайдемо за формулою:
S=½•AC•BKS=½•36•24=432(см²)
Відповідь: 432 см²
#SPJ1
c=\sqrt{a^2+b^2}=\sqrt{3^2+4^2}=5c=a2+b2=32+42=5 см
Радиус описанной окружности вокрруг прямоугольного треугольника равен
R=\frac{c}{2}=\frac{5}{2}=2.5R=2c=25=2.5 см
Длина окружности равна
С=2*\pi*R=2*3.14*2.5=15.7С=2∗π∗R=2∗3.14∗2.5=15.7 см
ответ: 15.7 см