ответ: 6√5 см
Объяснение:
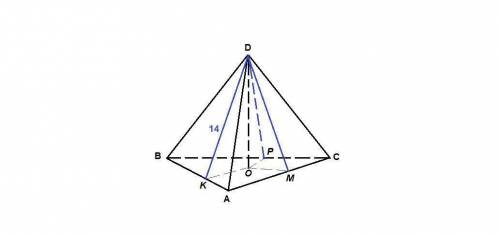
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
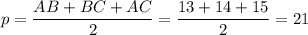
По формуле Герона
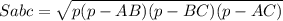
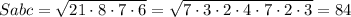 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см
Дано: АВСД - трапеция, ∠А=∠В=90°, ВС=20 см, СД=50 см; ∠ВСА=∠АСД. Найти S(АВСД).
∠САД=∠ВСА как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей АС.
∠САД=∠ВСА=∠АСД по условию, тогда ΔАСД - равнобедренный и АД=СД=50 см.
Проведем высоту СН. АН=ВС=20 см, ДН=АД-АН=50-20=30 см.
Тогда СН=40 см по свойству египетского треугольника.
S=(АД+ВС):2*СН=(20+50):2*40=1400 см²
ответ: 1400 см²